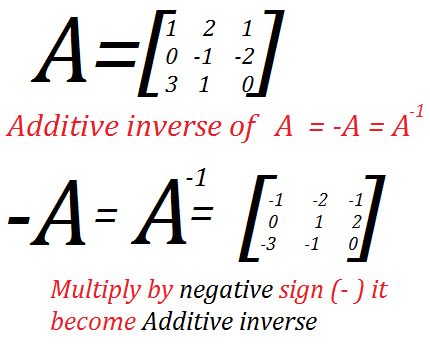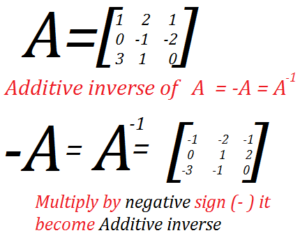Additive identity of a matrix example

by admin
Additive inverse of A

 

Additive identity of a matrix example:

Let’s consider a matrix A of size m x n. The additive identity of this matrix, denoted as 0, is a matrix of the same size where all elements are equal to zero. For instance, if A is a 3 x 3 matrix, then the additive identity matrix would be:

0 0 0<br /> 0 0 0<br /> 0 0 0

If A and B are two matrixes of same order and A + B = A  = B + A then the matrix B is called additive identity of matrix A.

Additive identity;

For any matrix A and zero matrix O of same order, is called Additive identity of A.

Additive identity of a matrix

Additive identity of a matrix example:

A + 0 = A = 0 + A

PROOF:

Let  Additive identity of a matrix

Then

Additive identity of a matrix

Additive identity of a matrix

Hence, this proves the A + O = A = O + A

Additive Inverse of Matrix A:

If A and B are two matrices of same order such That

A + B = O = B + A

then A and B are called additive inverse of each other.

Additive inverse of any matrix A is obtained by changing to negative of the symbol (entries) of each non-zero entries of A.

Additive inverse of A

Let \small A=\begin{bmatrix} 1 &2 &1 \\ 0 &-1 &-2 \\ 3 &1 & 0 \end{bmatrix}

Then

\small B= \left ( -A \right )=-\begin{bmatrix} 1 &2 &1 \\ 0& -1 & -2\\ 3 &1 & 0 \end{bmatrix}=\begin{bmatrix} -1 &-2 &-1 \\ 0 & 1 &2 \\ -3& -1&0 \end{bmatrix}\, is\, \, additive\, \, inverse\, of\, A

Hence, B is the Additive Inverse of A.

RELATED POST: