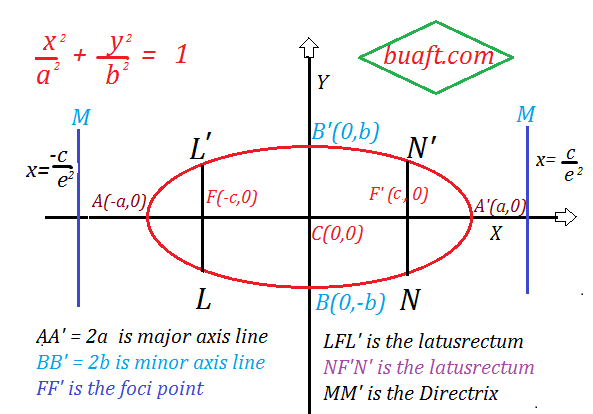
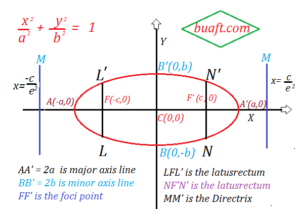
Foci of the ellipse:
Let F and F’ be two Foci of the ellipse, Foci of an ellipse are always lying on major Axis
x ²/ a² + y ² / b ² = 1
center of the ellipse:
Center of ellipse is the mid-point of two Foci point of an ellipse, here the coordinate of center C is (0, 0).
Vertices of an ellipse:
The end point on the ellipse on the x-axis, where y = 0 from figure these are the points A’ (-a, 0) and A (a, 0). The points A and A’ are called vertices of the ellipse.
Major axis of the ellipse:
The line segment AA’ = 2.a is called a major axis of the ellipse.
Minor axis of the ellipse:
The line through (1) and perpendicular to the major axis has its equation as x = 0. It means (1) at points B’ (0, b) and B(0, -b). The line segment BB’ = 2b is called the minor axis of the ellipse.
Covert ices of ellipse:
If b² = a ² (1 – e²) and e < 1 and the length of the major axis is greater than the length of the minor axis, then the figure on B. B’ is called co vertices of the ellipse.
Latusrectum and Latrarecta of the ellipse:
Each of the focal chords L F L’ perpendicular to the major Axis of an ellipse is called a Latusrectum of the ellipse. Thus, there are two Laterarecta of an ellipse. It is an easy exercise to find the length of the Latusrectum is 2 b² / a.
Foci lie on y-axis:
if the Foci lie on the y-axis with coordinate (0, -a.e) and (0, a.e) then the equation of ellipse is
x²/ b ²+ y ² / a² = 1 then a > b
RELATED POST:
- Standard form of an ellipse concept
- Standard equation of parabola proof
- ♣
- Parabola four type concepts standard form
- ♥
- Best definition of conic section
- ♦
- Reflecting property of parabola