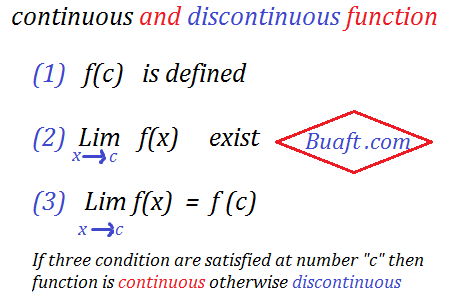continuous and discontinuous function

by admin
continuous and discontinuous function

Continuous and discontinuous function:A function f is said to be continuous at a number “c” if and only if the following three cases are satisfied:

continuous and discontinuous function

Three condition of continuous function

Discontinuous function:

If one or more of these three condition are fail to hold at “c” then function is said to be discontinuous function.

Continuous and discontinuous Function:

Example:

Consider the function:

f(x) =   x ² – 1 / x-1

or

(x -1)(x + 1) /x -1)

because

a ² – b ² = (a – b) (a + b)

Solution:

Here, f(1) is not defined

⇒  f(x) is discontinuous at 1.

Further

continuous function satisfy one

Therefore, f(x) is continuous at any other number whose x  ≠  1.

Continuous function example:

For f(x) = 3x² – 5x + 4

discuss continuity of “f”

at x = 1

SOLUTION:

continuous and discontinuous function

And

continuous and discontinuous function

continuous and discontinuous function

Therefore

f(x) is continuous at x = 1:

Discontinuous Function Example:

discuss the continuity of f

at x =3

f(x)    =    x-1,           if x  < 3

f(x)    =   2x  + 1,     if 3  ≤   1

Solution:

from the graph, we see that there is a break in the figure at the point when x = 3

Now      f(3)  = 2(3) + 1 =7

this implies that(⇒) condition (i) is satisfied

continuous function

continuous and discontinuous function

continuous and discontinuous function

That is, condition (ii) is not satisfied

discontinuous function

Hence, f(x) is not continuous at x = 3

RELATED POST