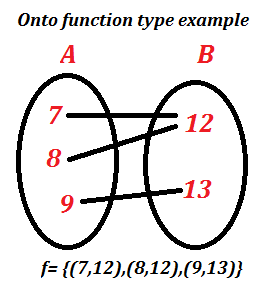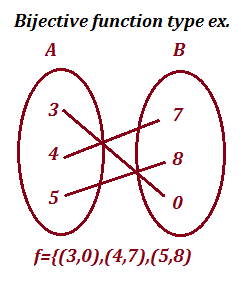Types of function example
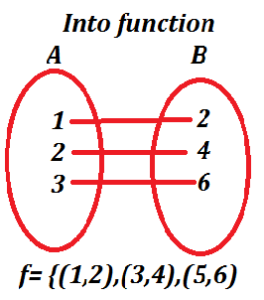
(1) Into function:
If function f such that A→B is such that Range f ⊂ B that is Range
f ≠ B then f is said to be a function from A into B
figure show that
f is clearly a function. But Ran f ≠ B
therefore, f is a functions for, A to B
(2) Onto function or(Surjective function):
if a function ƒ: A →B is such that Ran ƒ = B that is every element of B is the image of some element of A then ƒ is called an Onto function
Types of function example figure
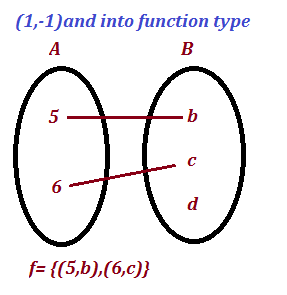
(3) INJECTIVE FUNCTION :
if a function ƒ from A to B is such that the second element of no two of its ordered pair are equal, then it is called an injective (1,-1 and into) function
From figure:
(4) (1, -1) and onto function (bijective function)
If ƒ is a function from A onto B such that the second element of no two of its ordered pairs are the same. Then f is said to be (1,-1) function from A to B
such the function is also called a (1,-1) correspondence between A and B. It is also called a bijective function.
RELATED POST