The standard equation of a parabola can be proved by considering the general equation of a parabola and transforming it into its standard form. The general equation of a parabola is in the form y = ax^2 + bx + c. By completing the square, we can rewrite this equation as y = a(x – h)^2 + k, where (h,k) represents the vertex of the parabola. This transformation allows us to identify the values of a, h, and k, which are crucial in determining the shape and position of the parabola. Thus, the standard equation of a parabola can be derived through this proof.
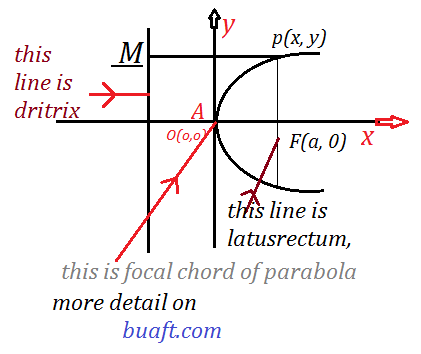
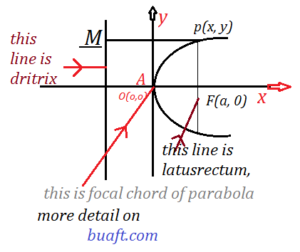
Standard equation of parabola proof, if we take focus of the parabola as F (a, 0), a > 0 (constant value of an is positive direction) and its DirectX as line L whose equation is x= -a then the equation become of the form
Let P (x, y) be a point on the parabola, so by definition.
…………. A
Now |PM| = x+a
and putting the value of B in A
……….. B
which is the standard equation of parabola
standard equation of parabola proof Definition:
(1) axis of the parabola
the line passes through the focus and perpendicular to the DirectX
is called axis of the parabola when y-axis = 0 that is y= 0
that is, y² = 4ax
(2) Vertex of the parabola
The point where the axis meet the parabola is called the vertex of the parabola
Clearly, the equation(C) has vertex A(0,0). The line through A and perpendicular to the axis
of the parabola has equation x = 0. It meets the parabola at a coincident point and
so it is tangent to the curve at A.
(3) Chord of the parabola:
A line joining two distinct point on a parabola is called a chord of the parabola.
(4) Focal chord of parabola:
A chord passing through the focus of a parabola is called the focal chord of the parabola.
(5) Latusrectum of the parabola:
The focal chord, perpendicular to the axis of the parabola from (1) is called latusrectum.
of the parabola.it has an equation x = a, and it intersects the curve at the point.
Where
y² = 4 a² or y = ± 2a
Thus, the coordinate of the end points L and L’ of the latusrectum are
L (a, 2a) and L’ (a, -2a)
The length of the latusrectum is |LL’| = 4a
(6) Parametric equation of the parabola
The point (at², 2at) lies on the parabola y² = 4 a.x for any real t.
X = at², y = 2at
are called parametric equation of the parabola
y² = 4ax