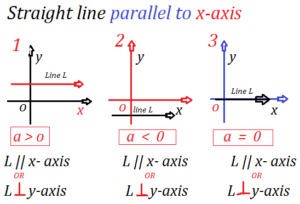
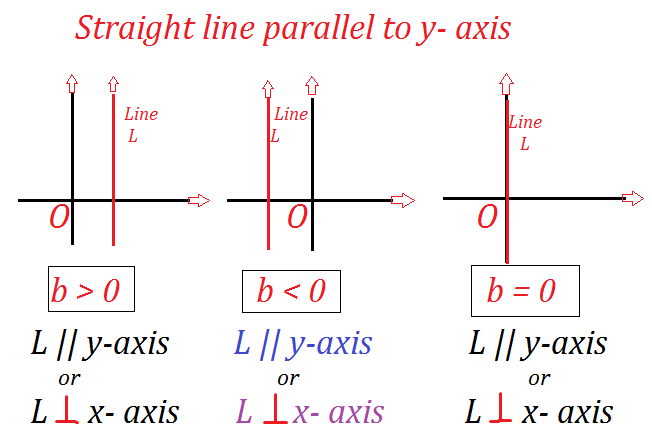Equation of straight Line parallel to the x-axis:
All the point on the Line L parallel to the x-axis remain at a common distance (say “a”) from the x-axis. Therefore, each point on the line has its distance from the x-axis equal to “a”. Which is its y-coordinate or ordinate. So all the point on this line satisfy the Equation:
Such that
| y=a |
Rule of Equation of straight Line parallel to x-axis:
| If a > 0 | Then the Line L is upper on x-axis |
| If a < 0 | Then the Line L is Lower on x-axis |
| If a = 0 | Then the Line L is becomes x-axis
Thus, the Equation of x-axis is y = 0 |
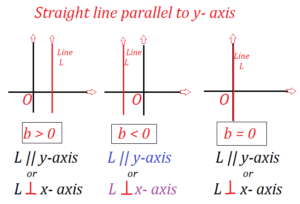
Equation of straight Line parallel to the y-axis:
All the point on the Line L parallel to the y-axis remain at a common distance (say “b”) from the y-axis. Each point on the Line has its distance from the y-axis equal to b. Which is its x-coordinate (abscissa). So, All the point on this Line satisfy the Equation.
| X = b |
Rule of Equation of straight Line parallel to y-axis:
| If b > 0 | Then the Line is on the right of the y-axis |
| If b < 0 | Then the Line is on the Left of the y-axis |
| If b = 0 | Then the Line becomes the y-axis
Thus, the Equation of y-axis is x = 0 |
RELATED POST
- equation of circle Cartesian plane
- ♣
- power of iota
- ♣
- Differential equation means and example
- ♣
- Cube root of unity power
- ♣
- Foci of the ellipse, covertices, major and minor axis
- ♣
- table of standard ellipse