Equation of circle Cartesian plane
The set of all points in the Cartesian plane that are equal distance from a fixed point is called a circle. The fixed point is called the center of the circle, and the distance from the center of the circle to any point on the circle is called the radius of the circle.
If C(h, k) is the center of a circle, r its radius and p(x, y) any point on the circle is denoted by notation
Center of circle notation
By distance formula we get
is an equation of the circle in standard form on the Cartesian plane.
Center of circle at origin
if the center of circle at origin, then equation of circle in standard form become.
Point circle
if r =0, the circle is called point circle.
Which consist of the circle only.
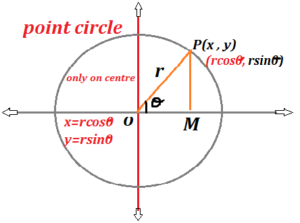
Parametric equation of circle
Let P(x, y) any point in the center of circle at origin
And let inclination of OP be θ (theta) in diagram
it is clear that
x= r cos θ
y= r sin θ
The point P (r cos θ, r sin θ) for all values of a theta (θ) are called parametric
equation of circle.
General form of an equation of circle on the Cartesian plane.
The equation
represent a circle g, f, and c being constant.
This equation can be written in the form
after simplification
which is the standard form of an equation of a circle with center (-g, -f)
and radius
Thus, equation A is called the standard form of an equation of circle.
RELATED POST
- COMPLEX Z PLANE
- INVERSE OF FUNCTION
- POWER OF IOTA finding
- 3.14159 is rational or irrational
- COMMUTATIVE PROPERTY OF RATIONAL NUMBER