intersection of two conic

by admin
intersection of two conic

Intersection of two conic:

Intersection between two conics hyperbola and parabolas are given.

Hyperbola equation in the form

x² / a²   – y² / b ²  = 1 ……….. A

and

parabola form is

y ² = 4ax………………. B

we fined the point common to both Equation (A) and Equation (B) we need to solve equation A and equation B simultaneously. We know algebra to solve the simultaneous solution set of two equation of the second degree consist of four points.

Thus, two conics will always interest in four points. These points may be all real and distinct, two real and two imaginary, or all imaginary.

Two or more points may also coincide:

Two conics are said to touch each other if they intersect in two or more confident point.

Intersection of two conic example:

intersection of two conic

conic equation: 1

\small \frac{x^{2}}{\frac{43}{3}}+\frac{y^{2}}{\frac{43}{4}} =1

This equation can be written in the form:

3x² +4y² = 43   …………… A

Conic equation 2 of hyperbola

\small \frac{x^{2}}{7}-\frac{y^{2}}{14}=1

we can write this equation in the form

2x² – y² = 14 ………………. B

Multiplying equation B by 4 and

adding the result into equation A. we get

11x² = 99

x = ± 3

putting x= 3 in equation B, we get result

18 – y ² = 14

y²  =  4

y = ± 2

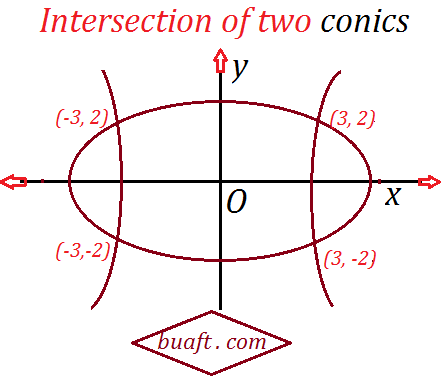
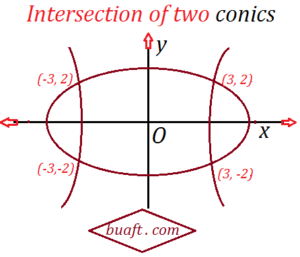
Thus, (3, 2)and (3, -2) are two point of intersection of the two conics.

And

putting x = -3 into equation B we get result

y = ± 2

therefore, (-3, 2) and (-3, -2) are also point of intersection

of equation A and B

RELATED POST