Conic section definition the best Let L be a fixed line in a plane and F be a fixed point not on the line L. suppose that |PM| denote the distance of the point p(x, y) from the line L. the set of all points Pin the plane such that |PF| ÷|PM|= e (positive constant) is called a conic section.
Conic section definition types best
(i) If e= 1, then the conic is parabola
(ii) If 0 < e < 1 then the conic is an ellipse.
(iii) If e > 1 then the conic is hyperbola.
The fixed line is called the directrix and the fixed point F is called a focus
of the conic. The number e is called the eccentricity of the conic.
General form of an equation of a parabola:
Let F(h, k) be the focus of the line, l x + my + n=0 be the DirectX of the parabola of a parabola. An equation of the parabola can be derived by the definition of the parabola.
Let P(x, y) be a point of the parabola. The length of the perpendicular PM from p(x, y) to the Directix is given by
that is
is a general form of an equation of the parabola.
Second degree equation of the form of parabola:
A second degree equation of the form
ax² + by²+2gx+ 2fy+ c=0
with either a= 0 or b =0 but not both zero, to represent a parabola the equation can be
analyzed by completing the square
Parabola types:
(1) if the focus lies on the y-axis with coordinate F(0, a) and directrix of the parabola
y= -a then equation of the parabola is
x² = 4ay
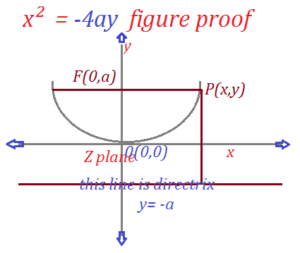
(2) if the focus is F(0,a) and directrix is the line y = a then the equation of the parabola is
x² = -4ay
(3) If the focus of the parabola is F (-a, 0) and its is the line x = a then the equation of the
parabola is
y² = -4ax
the curve is symmetric with respect to the x-axis and lies in the second and third quadrant.
RELATED POSTS

