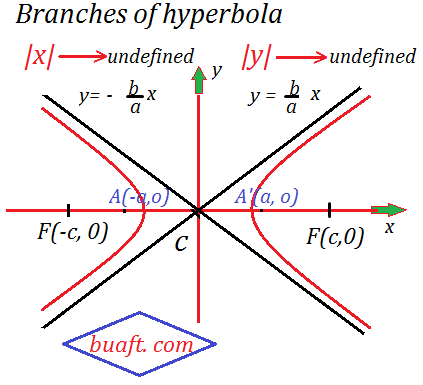
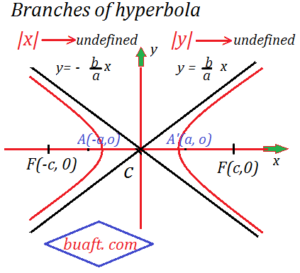
branches of curve of hyperbola

by admin
branches of curve of hyperbola

branches of curve of hyperbola: There are two branches of curve of hyperbola X² / a²  – Y² / b ² =1 we see this equation of hyperbola as | x| → ∞, | y |  → ∞ so we can extend branches to infinity and more detail by hyperbola equation.branches of curve of hyperbola image:

branches of curve of hyperbola→

x ² / a ²  –  y ² / b ²  = 1  …………………………. A 

The curve is symmetric with respect to both the axis. We can write equation A

 y ² / b ²  = x ² / a ²  –  1 

  y ² = b ² / a ²  (x ² –  a ²)

y = ± b / a √ x ² – a ²  …………………… B

branches of curve of hyperbola:

 (1) Branch of curve |x| < a 

If |x| < a, then y is imaginary so that no portion of the curve lies between

 (1) Branch of curve |x| < a 
(1) Branch of curve |x| < a

-a <  x  < a  For x  ≥  a ,

so that the point on the curve lies below the corresponding point on the line y = b / a (x)

in the first quadrant

branch of curve of hyperbola x  ≥  a
branch of curve of hyperbola x  ≥  a

And in this case the points on the curve lies

above the line \small y=\small \frac{-b}{a}\: x in the fourth quadrant.

Branches of curve of hyperbola

(2)Branch of curve |x| < – a

Branch of curve |x| < - a
Branch of curve |x|< – a

If x ≤ -a then, by similar arguments,

lies below the corresponding point

on  \small y=\small \frac{-b}{a}\: x   in second quadrant.

If   \small \small y = -\frac{b}{a}\sqrt{x^{2}-a^{2}}  then the curve lie above the corresponding point on \small \small y=\small \frac{b}{a}\: x in

third quadrant

Standard hyperbola table

Equation \small \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1 \small \small \frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1
Foci (± c, 0) (0, ± c)
Direct rices \small x= \pm \frac{c}{e^{2}} \small y= \pm \frac{c}{e^{2}}
trance verse axis y = 0 x =0
Vertices (± a , 0) (0, ± a)
Eccentricity e = c / a >  1 e = c / a >1
center (0, 0) (0, 0)

RELATED POST