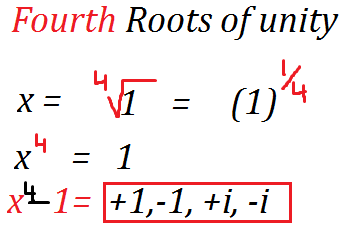Fourth Roots Of Unity Power

Fourth roots of unity power, take variable x equal to 1 root’s power 4 this gives the 4 roots +1, -1, +ι, -ι

X = ∜ 1

X= (1)¼

Suppose that

x be a fourth root of unity

Therefore

x=∜1
taking power 4 on both side
x⁴=(1)⁴×¼
after cancelation 4×1/4=1
one power 1 =1
we get
x⁴=1

X⁴ −1=0

we know the algebraic formula a²-b²=(a-b)(a+b)

⇒ (x² – 1)(x² + 1) = 0

⇒ (x² – 1) =0

x² = 1

x = ±1…………………1

⇒ (x² + 1) = 0

x² = – 1

x = ± ι……………………..2

Hence, the fourth root of unity are:

+1, – 1, + ι, – ι

Properties of four fourth roots of unity power 4

we have found that the four fourth root of unity are variable x power 4 = 1

+1, – 1, + ι, – ι

The sum of all the four fourth roots of unity power is zero

+1+(-1)+ι + (-ι) = 0

+1-1+ι-ι =0

Real fourth roots of unity are additive inverse of each other

+ 1 and – 1 are the real fourth root of unity

and

+ 1 + (-1) =0 = (-1) +1 (additive inverse of each other)

Complex or imaginary fourth roots of unity are conjugate of each other:

iota and – iota are complex or imaginary fourth root of unity

0 – ι conjugate equal to 0 + ι

Which is obviously conjugate of each other

Product of all the fourth Roots of unity is – 1

1 × (-1) × ι × (- ι) = -1

because ι² = – 1

Fourth roots of unity power