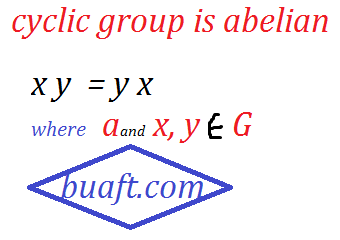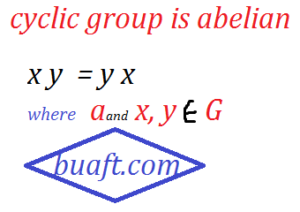cyclic group is abelian integers

by admin
cyclic group is abelian integers

Let G be a cyclic group is Abelian integers, generated by a (constant element) and x, y (variables) ∈ G. Then there are positive integers k and m such that

cyclic group is abelian integers

cyclic group is abelian integers

so

cyclic group is abelian integers

Thus, the group g is an Abelian group.

EXAMPLE:

If G is a cyclic group of even order, then prove that there is an only one subgroup of order 2 in G.

SOLUTION:

Let

\fn_cm G =< a:a^{2n}=e>

Be a cyclic group of order 2n, where n is a positive integer.

By proof, result G be a cyclic group of order n generated by a.then, for each

positive divider d of n, there is a unique subgroup (of G) of order d.

If a positive integer d divide |G|, then G has exactly one subgroup of order d.

Now

|G| = 2n and 2 divides 2n, so G has only one subgroup of order 2.

EXAMPLE:

Find all the subgroup of a cyclic group of order 12.cyclic group is abelian integers

Solution:

Let G be a cyclic group of order 12 and  ‘a’  be a generator. Then the elements of G are.

\fn_cm e = a^{12},a^{1},a^{2},a^{3},a^{4}........,a^{11}

By theorem

G be a cyclic group of order n generated by a.then, for each

positive divider d of n, there is a unique subgroup (of G) of order d.

1,2,3,4,5………..12

Therefore, G has

The subgroup of order 1 Which is {e}

The subgroup of order 2    Which is  \fn_cm \left \{ e,a^{6} \right \}

The subgroup of order 3  Which is \fn_cm \left \{ e,a^{4},a^{8} \right \}

The subgroup of order 4 which is \fn_cm \left \{ e,a^{3}a^{6},a^{9} \right \}

The subgroup of order 6  which is \fn_cm \left \{ e,a^{2},a^{4},a^{6},a^{10} \right \}

The subgroup of order 12 Which is  G itself.

RELATED POST:

properties of rings in groups

♠

unit and unity ring theory

♣

power series expansion

♣

Harmonic oscillator equation mass spring

♥

Reflecting property of parabola

♥

Foci of the ellipse, covertices, major and minor axis