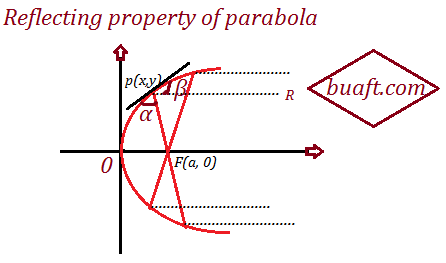
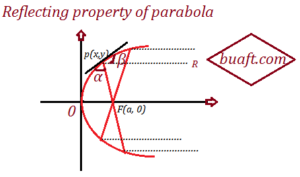
A frequently used property of a parabola is its reflecting property. If a light source is in place at the focus of a parabolic reflecting surface, then a light ray travelling from F to a point in the parabola will be reflected in the direction PR parallel to the axis of the parabola.
The designs of searchlights, reflecting telescopes and microwaves are based on reflecting property of the parabola.
Another application of the parabola is in a suspension bridge shape. The total weight of the bridge is uniformly distributed along its length if the shape of the cable is parabolic. Cables in any other shape will not carry the weight evenly.
Reflecting property of parabola example:
A suspension bridge with weight uniformly distributed along the length has two towers of 100 meters height above the road surface and are 400 meters apart. The cable are parabolic and are tangent to the road surface at the center of the bridge.
EXAMPLE:
We find the height of the cables at a point 100 m from the center.
Solution;
The parabolic formed by the cables has A(0,0) as vertex and focus on the y_axis.
An equation of this parabola is x² = 4 a y
The point Q (200, 100) lies on the parabola and so
(200)² = 4a × 100
a = 100
thus an equation of parabolic is
x² = 400 y ……… A
To find the height of the cables when x = 100 we have fro A
(100)² = 400 y
y = 25
Thus, required height 25 m.
RELATED POST:
- A circle passing through two point
- ♠
- tangential distance from p to circle
- ♣
- Tangents and Normal form ppt
- ♦
- Associative property of complex number