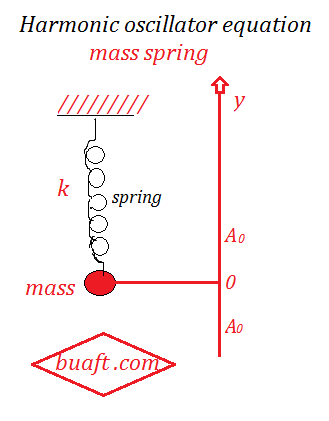Harmonic oscillator equation mass explain in the real world example, there are a number of quantities that oscillate or vibrate in a uniform manner, repeating themselves periodically in definite interval of time Some of the example are alternating electric current, sound waves, radio waves, light waves, pendulums, mass spring system, human heart beat, periodic variation, of the population of a plant or animal species.
The simplest mathematical models for such quantities is
y = A cos (ω t – φ)……………………………..(a)
where y is the oscillating quantity, t is time, usually measured in second, A is the positive constant, called amplitude of the oscillation, ω (omega) is a positive constant called angular frequency of the oscillation and Φ is a constant, called phase angle.
For each equation of the type (a), the constant v given by
v = w/ 2p
is called the frequency of the oscillation. If t is measured in seconds, then v represent the number of complete oscillations, called cycles per seconds. One cycles per second is called hertz (or Hz). The quantity T defined by
T = 1 / v
is called the period of the oscillation.
A quantity y oscillating in with the equation (a) is said to be undergoing a simple harmonic oscillation. Also, any device which produces a quantity that undergoes simple harmonic Oscillation is called a harmonic oscillator.
The harmonic oscillator equation
d²y /d²t + ω²y= 0 ……………………………..(b)
is obtained from (a) by differentiating the equation(a) twice. Hence, (a) is a solution of the differential equation (b).
The differential equation (b) is a second order linear differential equation and can be solved by the usual techniques of solving such solution.
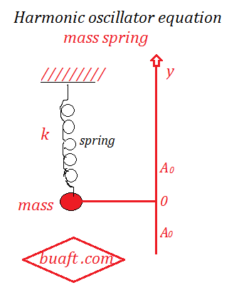
Mass spring system Example
suppose that a mass m is suspended by a perfectly elastic spring with spring constant k. The mass of the spring and air friction are neglected. A vertical axis y is set up so that when the mass and the spring are hanging in equilibrium, the mass is lifted to the position with y coordinate y =A ₀ and is released at time t = 0 with the initial velocity
V ₀ = 0, discuss the motion of particle, and we find
(i) the equation of the motion and (ii) the frequency of the oscillation
SOLUTION:
The mass moves ups and down between A ₀ and – A ₀, suppose that, at time t, the velocity of m is given by
v = d y / d t
and its acceleration is
a = d v / d t = d²y / d t²
by Hooke’s Law, the unbalance force F applied on a mass on a mass m by the spring is given by F – k y
so, by newton’s second law of motion, we have
F = ma = – k y
so that
a + k / m (y) = 0
d²y / d t² + k / m (y) = 0 …………………..(a)
is the differential equation of vibrating mass
Let k /m = ω² so that ω = √ k / m then (a) can be written as
d²y / d t² + ω y = 0
The general solution of differential equation is
y = A ₁ cos ω t + B ₁ sin ω t = A cos (ω t – Φ)
When t = 0, y(0) = A ₀, = A = √ A ₀² + 0² = A ₀, Φ = 0 so that the equation of motion is
y = A ₀ cos ω t = A ₀ cos ω √ k /m (t)
The frequency of the oscillation is, Harmonic oscillator equation mass
v = w / 2p = 1 / 2p √ k / m
RELATED POST
area under the curve integration
♣