Area under the curve integration concept about 300 B.C and around the mathematician succeeded to fined the area of the plane region like triangle, rectangle, trapezium and regular polygon etc. but the area of the complicated region bounded by the curves and the x-axis from x = a to x = b was a challenge for mathematician before the invention of integral calculus.
Now we give attention to the use of integration for evaluating areas. Suppose that a function f is continuous on interval a ≤ x ≤ b and f (x) > 0. To determine the Area under the graph f and above the x-axis from x = a to x = b. We follow the aria of Archimedes (287 – 212 B. C) for approximating the function by the horizontal function and the Area under f by the sum of small rectangles.
To explain the idea mentioned above, we draw the graph of f defined as
f(x) = 1/2 x²
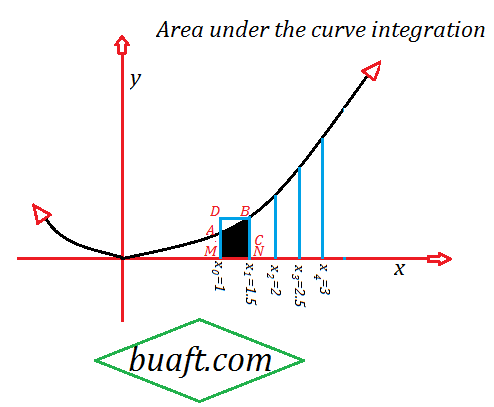
The graph of f is shown in the figure.
We divide the interval [1, 3] into four sub intervals of equal length = 3-1/2 = 1/2
As the sub interval are
[x ₀, x ₁], [x ₁, x ₂], [x ₂, x ₃], [x ₃, x ₄] and so
x ₀ =1, x ₁= 1.5, x ₂ =2, x ₃ = 2.5, x ₄ = 3
In the figure, MA = f(x ₀), NB = f(x ₁) and MN= δ x, so it is obvious that the area of the rectangle AM NC <the Area of the shaded region AM NB < the area of the rectangle DMNB that is,
that is f (x ₀) δ x less than the area of the shaded region AM NB < f(x ₁). δ x
Let x* ₁, x* ₂, x* ₃, x* ₄ be the mid-point of the four sub intervals mentioned above.
Then the value of f at x* ₁ is f(x* ₁) so the Area of the rectangle FM NE = f(x* ₁)δ x.
( see the rectangle FM NE shown in the figure)
we observe that the Area of the rectangle FM NE is approximately equal to the Area of the region AM NB under the graph of f from x ₀ to x ₁.
Now we calculate the sum of areas of the rectangles shown in the figure,
that is f(x* ₁)δ x+.f(x* ₂)δ x.+f(x* ₃)δx+.f(x* ₄)δ x.=[f(x* ₁)+.f(x* ₂).+f(x* ₃)+.f(x* ₄ )]δ x
=[½(x ₀+x ₁/₂)²+½(x ₁+x ₂/₂)²+½(x ₂+x₃/₂)²+½(x ₃+x ₄/₂)²]½
putting the values and solving it we get
= ¼[(1.25)²+(1.75)²+(2.25)²+(2.75)²]
by solving square all values and adding
= ¼ [17.25)= 4.3125
but area under the curve integration
₁∫³ ½ x²d x=[½ . x² /3 ₁]³= ⅙(27-1) = 26/6= 4.3
if we go on increasing the number of interval, then the sum of areas of small rectangles approaches closer to the number 4.3
if we divide the interval {1, 3} into n interval and take x* ₁ the coordinate of any point of the i th interval
and δ x ₁= x ₁ – x ᵢ − ₁ i = 1, 2, 3, 4 ………….n then sum of the areas of n rectangle is
which tends to the number 4.3 and when n→∞ and each δ x ₁ → 0