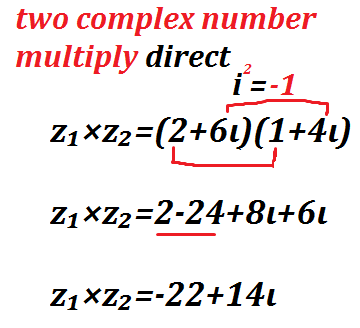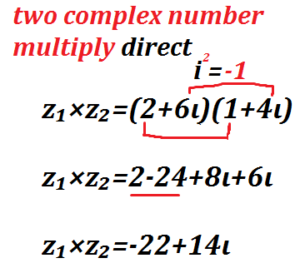complex number multiply

by admin
complex number multiply

Complex number is usually denoted by Z= (x, y) or z= x+ι y, complex number is the large number which is a group of all number. Natural number N, whole number W, set of integer Z, set of rational number Q, set of irrational number Q’, set of real number R. Complex number has two part (i) real part (ii) imaginary part. When we complex number, multiply two parts each other.

complex number multiply

Two complex number multiply

z1= x1+ ι y1

z2 = x2+ι y2

we simply multiply complex z1×z2 number each other

complex number multiply

applying  iota square =  -1   then 

y1y2   become – y1y2  (iota square application)

rearranging the real and imaginary part of multiplication

\large z_{1}\times z_{_{2}}=x_{1}x_{2}-y_{1}y_{2}+\iota x_{1}y_{2}+\iota y_{1}x_{2}

This is multiplication of two complex number.

Example of complex number multiplication

IF we have two complex number

Z1= 2+6i      and  

Z2 = 1+4i

Z1×Z 2    = (2+6i)(1+4i)

= 2+8i+6i-24

=   -22+14i

RELATED POST