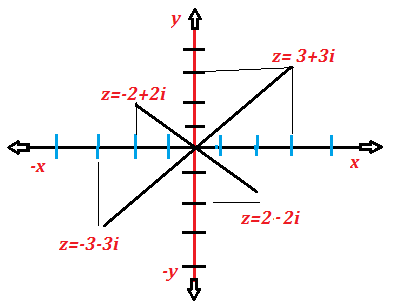
We have seen that there is a (1,-1) correspondence between the element (ordered pair) of the complex z plane RXR and the complex numbers. Therefore, there is a (1,-1) correspondence between the points of the complex z plane and the complex numbers. We can, therefore, represent complex number by the point of the coordinate plane. In this representation, every complex number will be represented by one and only one point of the complex z plane, and every point of the plane will represent one and only one complex number. The component of the complex number will be the coordinate of the point represent of the point representing it.
Complex Z plane
NOTE
coordinate plane is called the COMPLEX Z- PLANE or Argand PLANE
(i) Real x-axis
In representation of coordinate plane, X- AXIS is called real axis.
A point on the x-axis is called the real number
(ii) Imaginary, y-axis
In representation of coordinate plan plane, y- AXIS is called imaginary axis.
A point on the y-axis is called the imaginary number
(iii) x, y coordinate point
x, y are the coordinate of the point. It represents the complex number.
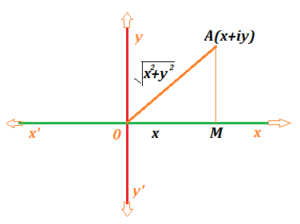
Modulus of complex number (a+ι b)
The real number is called the modulus of complex number a+ι b
modulus formula proof:
modulus of complex number a+Ι b
in the figure
(iv) Modulus of complex number sign |z|
modulus of complex number, generally denoted by
The modulus of the complex number is the distance from the origin of the point
representing the number.
modulus of z equal to
EXAMPLES OF MODULUS:
fined the modulus of the following complex number
(i) 1- ι√3
solution:
z= 1- ι√3
or z= 1- ι (√3)
this is equal to =
RELATED POST:
- INVERSE IF FUNCTION
- ♥
- 0.5555 is real number
- ♣
- proper and improper subset example
- ♣
- Kramer’s rule
- ♦
- Finite and infinite set ppt test
- ⇑
- Type of surd or irrational root definition and example
- ♥??????????????
- Power of iota
- ⊆
- properties of determinant proves