standard equation of hyperbola math

by admin
standard equation of hyperbola math 2

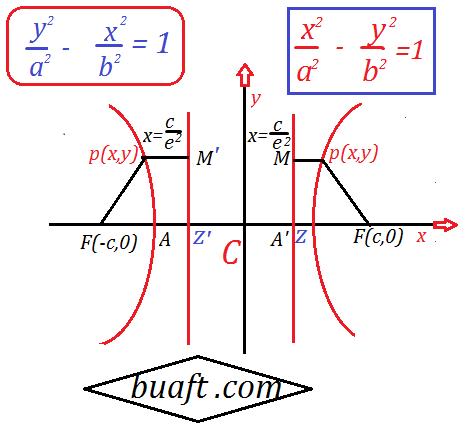
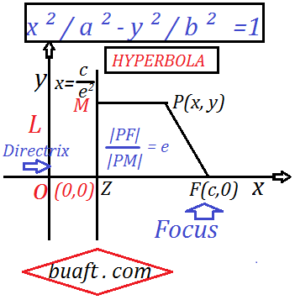
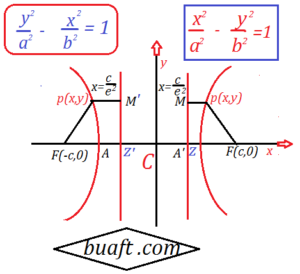
Let F(c,0) be the focus, with c > 0 and x = c / e² be the directrix of the hyperbola, also Let P(x, y) be a point on the hyperbola, by definition |PF| / |PM|  =e  is called standard equation of hyperbola in math proof ↓

that is,

standard equation of hyperbola math

(x – c)² + y ² = e² (x – c / e ²)

x ² – 2 x c + c ² + y ² = e ² x ² – 2 c x + c² / e ²

x ² (e ² -1) – y ²  =  c ² (1 – 1 / e²)

c ² / e ² (e ² -1)  ……………… B

Let us set a = c / e so that equation B become

x ²  (e ² -1) -y ² – a ² (e ² -1)  = 0

x ² / a ² – y ² / a ² (e ² -1)   =1

x ² / a ² – y ² / b ²   =1 …………….. (C)

where b ² = a ² (e ² -1) = c ² – a ²     because c = a. e

Equation (C) is a standard form of the hyperbola.

It is clear that the curve is symmetric with respect to both the axis.

If we take the point (-c, 0) as focus and the line x = -c / e ² as directrix

Then it is easy to see that the set of all point P(x, y) such that 

|PF| = e |PM| is hyperbola Form equation=x ² / a ² – y ² / b ²   =1

thus, a hyperbola has two foci and two direct rices.

If the Foci lies on y-axis, then role of x and y are interchange in x ² / a ² – y ² / b ² =1

then the equation of parabola become

standard equation of hyperbola math

y ² / a ² – x ² / b ²   =1

standard equation of hyperbola math 2

Definition:

The hyperbola

x ² / a ² – y ² / b ² =1 

meets the x-axis at a point with y = 0 and x = ± a. the point A(-a, 0)  and A'(a, 0)

are called the vertices of the hyperbola.

The line segment AA’ = 2Aa is called the Focal axis (transverse) of hyperbola, x ² / a ² – y ² / b ²   =1

The hyperbola x ² / a ² – y ² / b ²=1 does not meet the y-axis in real point.

However, the line segment joining the point B(0, -b) and B'(0, b) is called the 

Conjugate axis of the hyperbola.

The mid-point (0, 0) of AA’ is called the center of the 

hyperbola

In case of Hyperbola,

x ² / a ² – y ² / b ²   =1 

we have  b ² = a ² (e ² -1)= c² – a²

The eccentricity e = c / a  > 1

So that

Unlike the ellipse

We may have b > a    or       b  < a       or    b = a

Parametric Equation of hyperbola:

the point (a sec θ,   b Tan θ)  lies on the hyperbola x ² / a ² – y ² / b ²   =1

for all real value of θ. The Equation x = a sec θ,   y = b tan θ  are called parametric

Equation of Hyperbola.

Asymptotes of a curve:

Since   y   =  ±   b / a √ x² – a ²     modulus of |x| is very large

so that    x ² –  a² →  x ² we have

y  = ±  b / a (x)      that is   x ² / a²  – y ² / b ² …………. L

These lines L do not meet the curve but distance of any point on the curve from

any of the two lines approaches to zero. Such lines are called ASYMPTOTES of a curve.

Central Conic:

The ellipse and hyperbola are called central conic because each has a center of symmetry>

RELATED POST