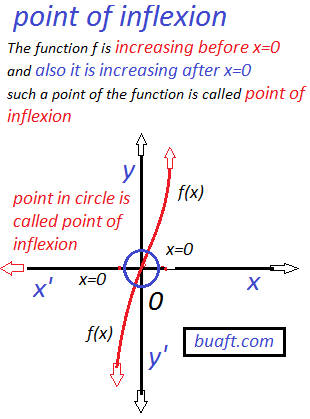
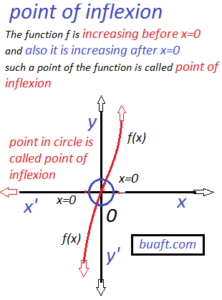
The function ƒ is increasing before x =0, and also it is increasing after x=0 such a point of the function is called the point of inflexion. Point of inflexion derivative rule detail:
NOTE:
(1) A stationary point is called turning if it either a maximum point or a minimum point.
(2) if ƒ’(x) >0 before the point x =a ,ƒ’(x) = 0 before the point x =a and ƒ’(x) >0 after x =a
then ƒ does not have a relative maxima.
See the graph of ƒ(x) = x³ in this case we have
ƒ’(x) =3x²
ƒ’(x)(0- ε) = 3(-ε)²= 3ε²>0
and
ƒ’(x)(0+ ε) = 3(ε)²= 3ε²>0
which point has these two conditions is called the point of inflexion.
Point of inflexion derivative rule:
What is the first Derivative rule:
Let ƒ be a differentiable in neighborhood where ƒ’(c)=0
Relative maxima of ƒ:
(1) if ƒ’(x) changes sign positive to negative as x increases through c, then ƒ(c)is the relative maxima of ƒ.
Relative minima of ƒ:
(2) if ƒ’(x) changes sign from negative to positive as x increases through c, then if ƒ’(c) is called the relative minima of ƒ.
RELATED POST:
- Differential equation means and example
- area under the curve integration
- implicit function symbolically and graph
- Finding common logarithm of any number
- x power zero equal one
- world power zero equal to 1