Implicit function symbolically and graph: if x and y are so mixed, cannot be expressed in terms of the independent variable is called an implicit function of x.

For example:
(i) x²+x.y+y²=2
(ii) x.y² -y+9 /x.y =1
are implicit function of x and y.
Symbolically, it has written as f(x, y)=0
Graphs of Implicit function:
(a) graph of circle of the form x²+y²=a²
Example 1: implicit function symbolically and graph
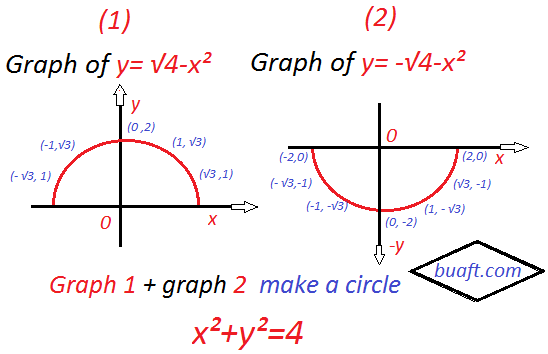
Graph of circle x²+y²=4 (1)
Solution:
The graph of equation x²+y²=4 is a circle of radius 2. Centered at origin and hence there are vertical lines that cut the graph more than once, this can also been seen algebraically by solving (1) for y in terms of x.
y = ±√4-x²
The equation does not define y as a function of x.
For example:
if x=1 then y= ±√3
hence (1,+√3) and (1,-√3) are two point on the circle and a vertical line passes through these two points.
We can regard the circles as the union of two semé circles.
y =√4-x² and y=– √4-x²
Each of which defines y as a function of x.
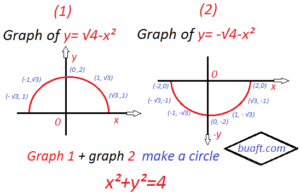
We observe that if we replace (x, y) in turn by (-x, y) and (-x, y)and (-x, -y), there is no change in the given equation. Hence, the graph is symmetric with respect to the y-axis and x-axis and the origin.
x=0 implies y²=4 ⇒ y=±2
x=1 implies y²=3 ⇒ y=±√3
x=2 implies y²=0 ⇒ y=0
by assigning values of x. we fined the value of y. so we prepare a table for some value of x and y satisfying equation (1)
Radius 2
if when x=2 then y=0
if when y=2 then x=0
| x | 0 | 1 | √3 | 2 | -1 | -√3 | -2 |
| y | ±2 | ±√3 | ±1 | 0 | ±√3 | ±1 | 0 |
plotting the graph (x, y) and connecting them with the smooth curve as shown in figure. We get a graph of the figure.
RELATED POST:
- variable in algebra formula
- Locus of a complex number definition
- composite and prime number factor
- world power zero equal to 1
- x power zero equal one