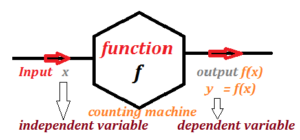
The variable x is called the independent variable of function f and variable y is called the dependent variable of function f. We clear the concept of dependent and independent variable of function by figure
REAL VALUED FUNCTION:
For now onward, we shall only consider the function in which the variables are real numbers, and we say that f is a real value function of real number
Real valued function example
EXAMPLE:
We have the function f(x) = x³-2x²+4x-1
(i) f(0) = ?
f (x) = x³-2x²+4x-1
f(0)=0-0+0-1= -1
(ii) f(1) =?
f (x) = x³-2x²+4x-1
f(1) = 1-2+4-1 = +2
(iii) f(-2) = ?
f (x) = x³-2x²+4x-1
f(-2)= (-2)³-2(-2)²+4(-2)-1
= – 8- 8-8-1= -25
(iv) f(1+x) =?
f (x) = x³-2x²+4x-1
f(1+x)= (1+x)³-2(1+x)²+4(1+x)-1
f(1+x) = x³+x²+3x+2
(v) f(1/x) =? Where x ≠ 0
f (x) = x³-2x²+4x-1
f(1/x)=(1/x)³-2(1/x)²+4(1/x)-1
= 1/x³-2/x²+4/x-1 Where x ≠ 0
Function notation:
if a variable y depends on a variable x in such a way that
each value of x determine exactly one value of y, then we say that
“y is a function of x”
Swiss mathematician Euler(1707-1783) invented a symbolic way to
write the statement “y is a function of x”
as y=f(x) which read as” y is equal to x”
Explanation of function:
A function can be considered as a computing machine f that takes an input x,
exactly one output f(x). This output f(x) is called the value of f at x or image of x under f.
The output f(x) is denoted by a single letter, say y, we write y= f(x)
Definition of function, domain, range
A function f from a set X to a set Y is a rule or a correspondence that assigns
to each element x in X a unique element y in Y. the set X is called the Domain of f.
The set of corresponding element y in Y is called the Range of f.
RELATED POST