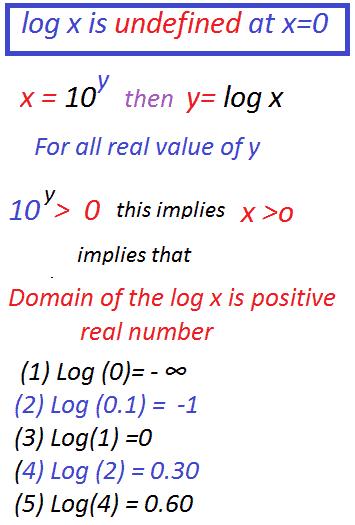Log x is undefined at x equal to 0 : If x= 10 power y, 10 power y greater than zero, this implies that x greater than zero. This means that log x exist only when x greater than zero. This implies that the Domain of the log x is a positive real number.
Log x is undefined at x equal to 0 image:
Resultant Note:
log x is undefined at x=0
For the graph of y= f(x) = log x, we fined the value of log x from the common Logarithm table for various values of x greater than zero.
Values of Log x
Log of zero
(1) Log (0)= – ∞
Log of 0.1
(2) Log (0.1) = -1
log of 1
(3) Log(1) =0 where x always values greater than zero.
Log of 2
(4) Log (2) = 0.30
Log of 4
(5) Log(4) = 0.60
A table of some of the corresponding values of x and f(x) is shown.
| x | →0 | o.1 | 1 | 2 | 4 | 6 | 8 | 10 | → +∞ |
| y=f(x)= Log | →-∞ | – 1 | 0 | 0.30 | 0.60 | 0.77 | 0.90 | 1 | → +∞ |
Values of Exponential Function:
As the approximate value of “e” is 2.718
the graph of “e power x” has the same characteristic and the properties of “a power x”when a > 1
Exponential power zero
Exponential power one
Exponential power two
Exponential power -1
Exponential power -2
Exponential power -3
RELATED POST:
- log rule exponential of real number
- logarithm laws of real number
- Mantissa of logarithm of real number
- Finding common logarithm of any number