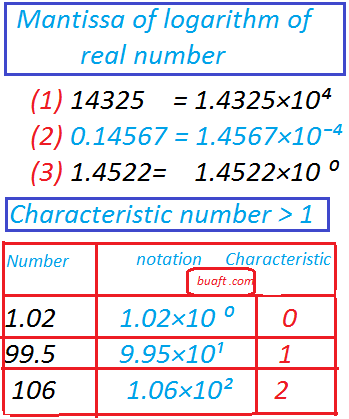
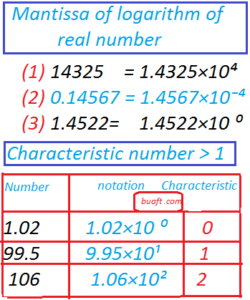
A decimal part, which is always positive, is called the mantissa of the logarithm of the real number.Mantissa of logarithm of real number defined below.
An integral part which is positive or “a number greater than 1 and negative part for a number less than 1, is called characteristic of logarithm of number.
Observation:
The logarithm of any number consist of two part, which has been described before.
(i) 14325= 1.4325×10⁴
(II) 0.14567= 1.4567×10⁻⁴
(III) (3) 1.4522=1.4522×10 ⁰
Characteristic of Logarithm of a real number greater > 1
The first part of the above table shows that if a number has one digit in the integral part, then the characteristic is 0; if its integral part has two digits, then the characteristic is 1 ; with three digits in the integral part, the characteristic is 2 and so on.
Observe:
The characteristic of the logarithm of a number greater than 1 is always 1 less than the number of digit in the integral part of the number.
Mathematical notation writing method;
when a number b is written in scientific notation:
b= a×10 ⁿ
where 1 ≤ a ≤ 10,
the power of 10 will give the characteristic of the log b.
Example:
| Number | mathematical notation | Characteristic of logarithm |
| 1.02 | 1.02×10 ⁰ | 0 |
| 99.5 | 9.95×10¹ | 1 |
| 106 | 1.06×10² | 2 and so on |
Characteristic of Logarithm of a real number less < 1
A number has no zero immediately after the decimal point, the characteristic is -1,
if it has one zero immediately after the decimal point, the characteristic is -2.
If it has two zero immediately after the decimal point, the characteristic is -3; and more so on.
Characteristic less than 1 example.
Example:
| Number | mathematical notation | Characteristic of logarithm |
| 0.472 | 4.72×10 ‾¹ | -1 |
| .03 | 3.0×10⁻² | -2 |
| 0.00445 | 4.45×10⁻³ | -3 and so on |
Characteristic of logarithm symbolically < 1 written as
we write -3 symbolically 3‾
we write -2 symbolically 2¯
we write -1 symbolically 1‾
Mantissa of logarithm of real number in table.
Fined the mantissa of logarithm of 43.254
rounding off 43.254
we consider only four significant digit 4325.
(1) we see rows corresponding to 43 in log table.
(2) see horizontally till we reach the column 2.the number at the intersection is 6355.
(3) again proceeding horizontally till the mean difference column corresponding to 5 intersect this row. We get the number 5 at the intersection.
(4) Adding the two number 0.6355 and 5.
We get 0.6360 as the mantissa of the logarithm.
RELATED POST:
- log rule exponential of real number
- Cube root of unity power
- Fourth roots of unity power
- implicit function symbolically and graph