Line segment dividing the point

by admin

Line segment dividing the point: Let A (x ₁, y ₁) and B(x ₂, y ₂) be the given two point in a plane. The coordinate of the point dividing the line segment AB in the ratio K ₁:k ₂ are
(k ₁ x ₂+k ₂ x ₁÷ k ₁ + k ₂ , k ₁ y ₂+ k ₂ y ₁÷k ₁ +k ₂)

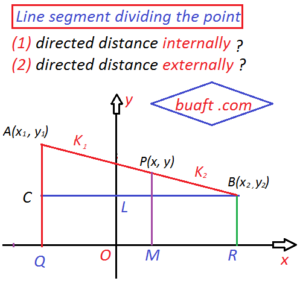
PROOF:

Let P(x, y) be the point that divide AB in the ratio k ₁ +k ₂.

From A, B and P draw perpendicular to x-axis as shown in the figure

Also draw BC perpendicular A Q

Since LP is parallel to CA, in the triangle ABC we have

$\frac{k_{1}}{k_{2}}=\frac{AP}{BP}$

$\frac{AP}{PB}=\frac{CL}{CB}$

$\frac{CL}{CB}=\frac{QM}{MR}$

$\frac{QM}{MR}=\frac{x-x_{1}}{x_{2}-x}=\frac{k_{1}}{k_{2}}$

after checking ratio

$so\, \, \, \, \frac{k_{1}}{k_{2}}=\frac{x-x_{1}}{x_{2}-x}$

K ₁ x ₂ – k ₁ x = k ₂ x – k ₂ x ₁
or
(k ₁ + K ₂) x = k ₁ x ₂+ k ₂ x ₁
or
x = k ₁ x ₂ – k ₂ x ₁/ k ₁ + K ₂

Similarly, by drawing perpendicular from A, B and P to the y-axis and proceeding as before we can show that.

y = k ₁ y ₂ – k ₂ y ₁ / k ₁ + K ₂

(1) Directed distance internally:

If the directed distance AP and BP have the same sign , then the ratio is positive and P is said to divide AB internally.

(2) Directed distance Externally:

If the directed distance AP and BP have the opposite sign ,that is P is beyond AB, then the ratio is negative and P is said to divide AB Externally.

$\frac{AP}{BP}=\frac{k_{1}}{k_{2}}$ or $\frac{AP}{PB}=\frac{k_{1}}{k_{2}}$

Proceeding as before, we can show in this case

x = k ₁ x ₂ – k ₂ x ₁/ k ₁ + K ₂

y = k ₁ y ₂ – k ₂ y ₁ / k ₁ + K ₂

Thus, P is said to divide the line segment AB in ratio k ₁ : K ₂

Externally, according as P lies between AB or beyond AB.

(3) If k ₁ : K ₂= 1:1, then P the mid-point of AB and the coordinate of P are

such that

$x=\frac{x_{1}+x_{2}}{2}\,\,, y= \frac{y_{1}+y_{2}}{2}$

RELATED POST:

Related