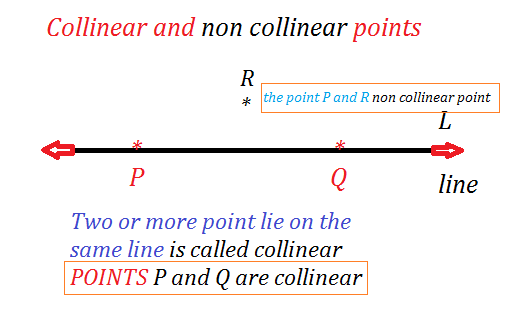Collinear and non-collinear point in the plane, two or more points which lie on the same straight line are called collinear points with respect to that line and outside the point of the line are called non-collinear points.
Let L be a line, then all point on the line L are collinear point.
In the given figure the point P, and Q, are collinear point with respect to the Line L and the point P and R are not collinear with respect to the line.
Collinearity of three or more point in the plane:
Let P, Q and R are three point in the plane They are called collinear
If |PQ|+ |QR|= |PR| otherwise they are not collinear.
EXAMPLE:
Using distance formula show that the points collinear or non-collinear
(I) P(-2, -1), Q(0, 3), And R(1,5)
|PQ| = √(0+2)²+(3+1)²= √4+16 =√20 = 2√5
|QR| = √(1-0)²+(5-3)²= √1+4 = √5
and
|PR| = √(1+2)²+(5+1)²= √9+36 =√45 = 2√5
We see that |PQ|+|QR|= 2√5 + 2√5 = 3√ 5 = |PR|
Therefore, the points P, Q and R are collinear.
EXAMPLE:
The points P(-2, -1), Q(0, 3), R(1,5) and S(1, -1) are not collinear.
|PS| = √(-2-1)²+(-1+1)²= √9+ 0 = 3
Since |QS| = √(1-0)²+(-1-3)²= √1+16 =√17
and
|PQ| + |QS| ≠ |PS|
Therefore, the points P, Q, and S are not collinear.
And hence, the points P, Q, R and S are also not collinear.
A closed Figure in a plane obtained by joining three non-collinear point
is called Triangle.
Vertices of triangle:
In the triangle ABC the non-collinear points A, B, and C are the
three vertices of the triangle ABC.
The line segment AB, BC and CA are called side of the triangle.
RELATED POST