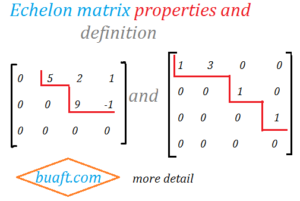
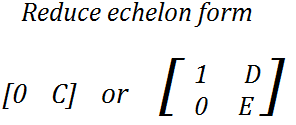Echelon matrix properties and definition, An m × n matrix A is said to be in (row) echelon ¹ form (or an echelon matrix) if it has the following properties.
(i) All non-zero rows are above any zero rows ( consisting of all zeros)
(ii) The first nonzero entry in each non-zero row is to the right of the first nonzero entry of each preceding row. That is, the number of zeros occurring before the first non-zero entry in each non-zero row is greater than the number of zeros that appear before the first non-zero element in any preceding row.
PIVOT or row leader:
In an echelon matrix, the first non-zero entry of a row is called a PIVOT (or a row leader). There is at the most one pivot in each row and in each column of an echelon matrix
pivot column:
A column consisting of a pivot is called a pivot column.
Row reduced echelon form.
An echelon matrix in which each pivot is 1 and every other entry of the pivot column,
is said to be row reduced echelon form. Are in echelon form. The second matrix is in row
Theorem: ;Echelon matrix properties and definition by theorem
Every matrix is a row equivalent to a matrix in echelon form (reduce echelon form)
PROOF:
Let A be a given m × n matrix. Either every element in the first column of A is zero or there exist non-zero element ‘a’ in the kith row, of this column. In the second case, interchanging the first and ‘kth’ rows of A, we obtained matrix B. whose first element b ₁ ₁ = a ≠0. Multiplying the element of the first Row of B by a. inverse. We obtained a matrix C whose first entry c ₁ ₁= 1. By adding proper multiplies of the first rows of C to the other rows, the reaming element of the first column can be made zeros. In the first case, we considered the second column and so on till we fined a column with a nonzero entry. We then repeat the process as for the second case. Thus, A is a row equivalent to a matrix in either of the forms
Where, in the first case, 0 represent the m× 1 zero matrix and C an m× (n-1) matrix.
In the second case, 0 represent the (m – 1)zero matrix, D a 1 ×(n – 1) matrix and E an(m – 1) × (n – 1).
In the first case, repeat the above process with the matrix C,
whereas in the second case repeat the process with matrix E. A continuation of this process lea to the desired form.
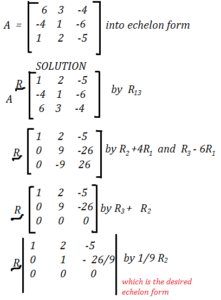
EXAMPLE: Reduce to the matrix
RELATED POST:
area under the curve integration
Harmonic oscillator equation mass spring