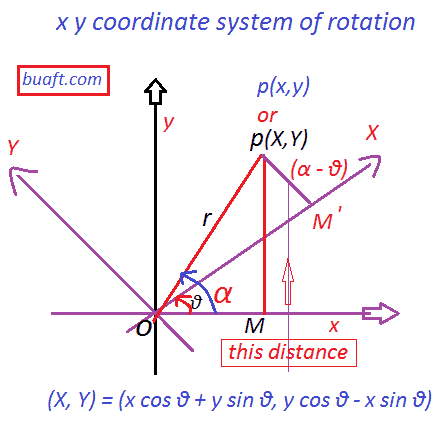
x.y coordinate system of rotation: Let x y coordinate system be given. We
We rotate the x y coordinate system about the origin through an angle θ, where 0 < θ < 90°, resulting in the new axes O. X and O. Y. Consider a point P with coordinates (x, y) in the x y system. Let (X, Y) be the coordinates of point P in the X Y coordinate system. We need to find X and Y in terms of the given coordinates x and y. α represents the angle that OP makes with Ox.
about the origin through an angle θ means 0< θ < 90° so that the new axis are O.X and O.Y as shown in the diagram. Let a point P has coordinated (x, y) referred to the x y system of coordinates. Suppose p has coordinated (X, Y) referred to the X Y coordinate system. We have to fined X, Y in terms of the given coordinate x, y. Let α be a measure of the angle that OP makes Ox.
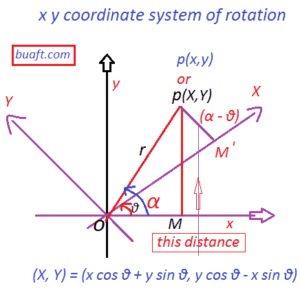
x y coordinate system of rotation proof:
From P, draw PM perpendicular to ox and PM and perpendicular to Ox.
Let | OP | =r. From the right angle ∆ OPM‘ we have
OM’ =X = r cos (α – θ)………………..(1a)
M’P= Y= r cos (α – θ)………………..(1b)
these equations can be written as
X = r cos α cos θ + r sin α sin θ
Y = r cos α cos θ – r sin α sin θ
Also, from the ∆ OPM we have
x = r cos α y = r sin α ………..(2)
Equation 2 can be written as
r = x / cos α and r = y / sin α
Putting the value of 2 in equation 1 we get the result
X = x cos θ + y sin θ
Y = y cos θ – x sin θ
that become
(X, Y) = (x cos θ + y sin θ, y cos θ – x sin θ)
are the coordinate of P referred to the new axis OX and O Y.
RELATED POST: