Tangents and Normal form ppt

by admin

tangent and normal form ppt

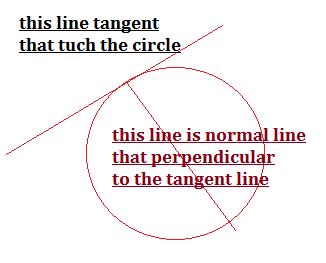
Any line that touch any curve or slope in any side is called tangent, in other words, A tangent to a curve is a line that touch the curve without cutting through it. Tangents and Normal form ppt.

We know that for any curve whose equation is given by y= f(x) or f(x, y) = 0 the derivation d y / d x is the slope of the tangent at any point P(x, y) to the curve. The equation of the tangent to the curve can easily be written by the point slope formula .

Any line that perpendicular to the tangent line at any point or any side is called a normal line. In other words, the normal line to the curve at P is the line through P perpendicular to the tangent to the curve at P. this method can be very conventicle employed to fined of equation of tangent and normal form ppt to the circle.

Tangents and Normal form ppt image.

at the point $at the point$

Here

f(x, y) = ……………….. A

differentiating (1) w, r, t, x, we get

2x +2 y d y/d x+2g + 2f d y / d x =0

$\frac{dy}{dx}= - \frac{x+g}{y+f}$

if slope of tangent at point $at the point$

$\frac{dy}{dx}]_{x_{1},y_{1}}= \frac{x_{1}+g}{y_{1}+f}$

Hence, the equation of tangent at point p is with point slope form

${y-y_{1}}= -\frac{x_{1}+g}{y_{1}+f}\left ( x-x_{1} \right )$

algebraic simplification

$y(y_{1}+f)-y_{1}^{2}-y_{1}f=-x(x_{1}+g)+x_{1}2+x_{1}g$

$xx_{1}+yy_{1}+gx+fy=x_{1}^{2}+y_{1}^{2}+gx_{1}+fy_{1}$

adding both side $gx_{1}+fy_{1}+c$ after implication

$xx_{1}+yy_{1}+g(x+x_{1})+f\left ( y+y_{1} \right )+c=0$

since $\left ( x_{1}, y_{1} \right )$ lies on A and so on

$x_{1}^{2}+y_{1}^{2}+2gx_{1}+2fy_{1}+c=0$

$xx_{1}+yy_{1}+g(x+x_{1})+f\left ( y+y_{1} \right )+c=0$

Is the required equation of the tangent form ppt.

Equation of normal at P

we fined an equation of the normal at P. We take the negative reciprocal of the slope of the tangent.

$\frac{y_{1}+f}{x_{1}+g}$

equation of normal at point $at the point$ is

$y-y_{1}=$ $\frac{y_{1}+f}{x_{1}+g}$ $\left ( x-x_{1} \right )$

thus the equation of the normal line is

$\left ( y-y_{1} \right )\left ( x_{1}+g \right )=\left ( x-x_{1} \right )\left ( y_{1}+ f\right )$

required equation of normal form ppt

RELATED POST

a circle passing through two point