Signs of trigonometric function theta: If theta θ is not a quadrant angle, then it will lie in a particular quadrant. Because r = √ x²+y² is always positive, it follows that the sign of the trigonometric function can be found if the quadrant of θ is known.
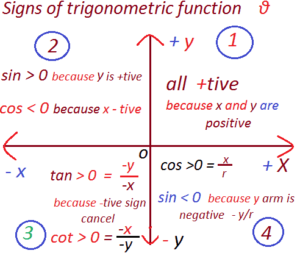
Signs of trigonometric function theta laws:
(1) First quadrant sign:
If theta lies in quadrant 1,then a point p(x, y) on its terminal side has both x, y co-ordinates +time.
 .
.
Resultant: All trigonometric functions are positive in first quadrant.
(2) Second quadrant sign:
If theta lies in quadrant ii, then a point p(x, y) on its terminal side has negative x – co-ordinate and positive y-co-ordinate.
Resultant sign:
sin θ = y / r =positive
cos θ = x / r = negative < 0 (because adjacent side is negative) cos θ always lies on x-axis.
Tan θ = y / x = negative <0 (because one of the sign x-axis is negative)
(3) Third quadrant sign:
If theta lies in quadrant iii, then a point p(x, y) on its terminal side has negative x – co-ordinate and negative y-co-ordinate.
Resultant sign:
sin θ = y / r =negative <0 (because arm y is negative)
cos θ = x / r = negative < 0 (because adjacent side x-axis is negative) cos θ always lies on x-axis.
Tan θ = y / x = positive >0 (because two negative sign cancel each other).
(4) Fourth quadrant sign:
If theta lies in quadrant iv, then a point p(x, y) on its terminal side has positive x co-ordinate and negative y-co-ordinate.
Resultant sign:
sin θ = y / r =negative < 0 (because arm y is negative)
cos θ = x / r = positive > 0 (because adjacent side is positive) cos θ always lies on x-axis.
Tan θ = y / x = negative <0 (because one of the sign y-axis is negative).
RELATED POST:
- Trigonometric identities of any real number theta
- circular radius of length theta
- Sexagesimal system Degree minute second
