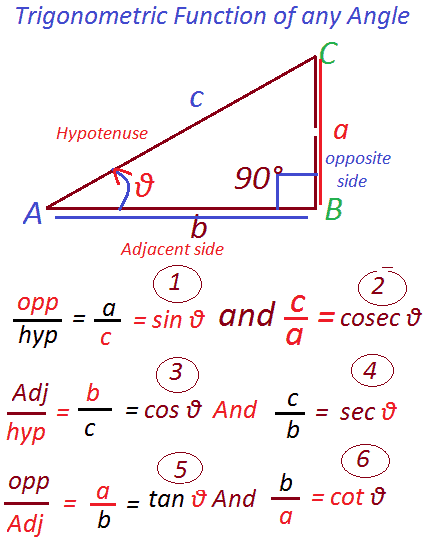
Trigonometric Function of any Angle:Consider a right Angle Triangle ABC with Angle ∠ C =90° and side a, b, c as shown in the Figure.
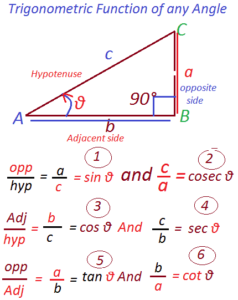
Let m ∠ A = θ Radian
(1) the side AB opposite to 90° is called Hypotenuse.
(2) The side BC opposite to θ is called the opposite side, the side AC
(3) The side AC related To Angle θ is called Adjacent side.
We can be shown 6 ratios as:
a÷b mean a / c
b÷c means b / c
a÷b means a / b
c ÷ a means c/ a
c ÷ b means c / b
b ÷ a means b / a
Why ratio are called trigonometric function:
In fact, these ratios depend on only the size of the Angle and not on the Triangle formed. There these ratios are called trigonometric function of Angle θ and defined as down.↓
Trigonometric basic Angle:
(1) Sine θ : sin θ= a / c = opposite/hypotenuse.
Reciprocal Angle
Cosecant θ : sin θ= a / c = hypotenuse/opposite
(2) cosine θ : cos θ= b / c = Adjacent/hypotenuse.
Reciprocal Angle
Secant θ : sec θ= c / b =hypotenuse / Adjacent.
(3) tangent θ : tan θ= a / b = opposite/ Adjacent.
Reciprocal Angle
cotangent θ : cot θ= b / a =Adjacent/opposite.
Observation Angle:
cosec θ = 1 / sin θ
secθ =1/cosθ
tanθ =sinθ/ cosθ
cotθ= cosθ/ sinθ
cotθ = 1/ tanθ
RELATED POST:
- circular radius of length theta
- Initial side and terminal side angle
- Initial side and terminal side angle