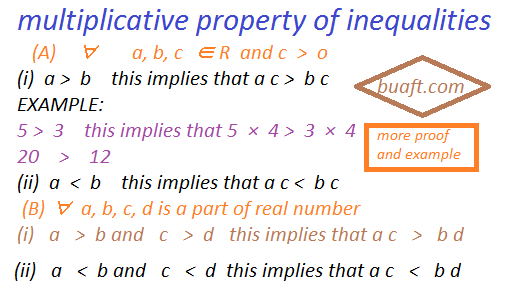Multiplicative property of inequalities, For all number a, b, c, d (maybe any numeric number 2, 3, 4, 5) is a part (∈) of real number (R). We divide multiplicative property of inequalities in three part and discuss one by one.
(a) multiplicative property of inequalities
∀ a, b, c ∈ R and c > o
When number a greater than number b and third number c greater than zero, then the property of inequalities
(i) a > b this implies that a c > b c
Addition and multiplication laws of real number?
(ii) a < b this implies that a c < b c
EXAMPLE:
∀ 5, 3, 4 ∈ R and 4 > o
associative property of real number ???????
We have numbers, a = 5, b= 3 and third number c = 4 greater than zero, then the property of inequalities
(i) 5 > 3 this implies that 5 × 4 > 3 × 4
20 > 12
(ii) a < b this implies that a c < b c
if numbers a = 3, b = 5 and c = 4
3 < 5 this implies that 3 × 4 < 5 × 4
12 < 20
(b) ∀ a, b, c is a part of real number and c < 0
(i) a > b this implies that a c < b c
(ii) a < b this implies that a c > b c
EXAMPLE:
We have numbed a = 5, b = 4 and c = – 2 then condition
(i)
5 > 4 this implies that 5 × -2 < 4 × -2
-10 < -8 (proved)
EXAMPLE: power of iota ?
We have numbered a = 5, b = 6 and c = – 2 then condition (ii)
5 < 6 this implies that 5 × -2 > 6 × -2
-10 > – 12 (proved)
(C) ∀ a, b, c, d is a part of real number, and a, b, c, d are all positive
(i) a > b and c > d this implies that a c > b d
(ii) a < b and c < d this implies that a c < b d
EXAMPLE: branches of curve of hyperbola ???????
If 3, 4, 5, 6 is a real numbers then condition (i)
3 > 4 and 5 > 6 this implies that 3 × 5 > 4 × 6
15 > 24 proved
EXAMPLE:
If we have real number a = 5, b = 4, c = 3 and d = 2 then condition (ii)
5 < 4 and 3 < 2 this implies that 5 × 3 < 4 × 2
15 < 8 proved
RELATED POST: