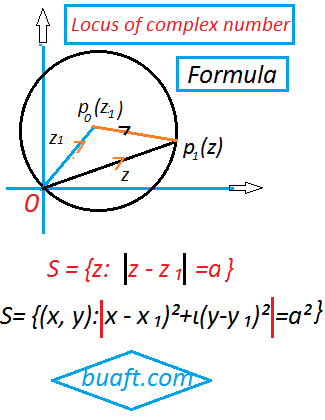Locus of a complex number definition:
Let P(z) be a property satisfied by a complex number Z = x+ι.y. For example, a complex number may satisfy the condition modulus of Z means ∣z∣=2
the set
S= {x:∣z∣=√ x²+y²=2}
🙁 means such that)
x:∣z∣ (means x is a set such that modulus of z)
S= {(x, y):x²+y²}=4
is called the locus of the complex number Z definition.
satisfying ∣z∣=2
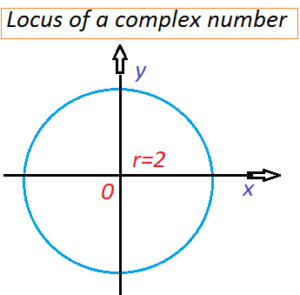
In the figure, the locus of z represent a circle with center at (0, 0)and radius 2 (r =2)
Locus of a complex number example:
we fined the locus of the complex number z = x+ι.y,
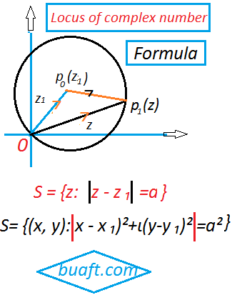
such that for a fixed point
z ₁ = x ₁ + ι y ₁, ∣z ₁- z ₂ ∣= a
From figure, we have →p ₒ p ₁=∣‾ p ₒ p ₁∣=∣z – z ₁∣= a
S = {z: ∣ z – z ₁∣ =a
S= {(x, y):∣x – x ₁)+ι (y – y ₁)∣=a
S= {(x, y):∣x – x ₁)²+ι(y-y ₁)²∣=a²
Which is a circle with center at Z ₁=(x ₁+y ₁) and radius r= a
RELATED POST:
- x power zero equal one
- complex z plane
- power of iota
- radicals and radicands
- least common prime factor
- composite and prime number factor