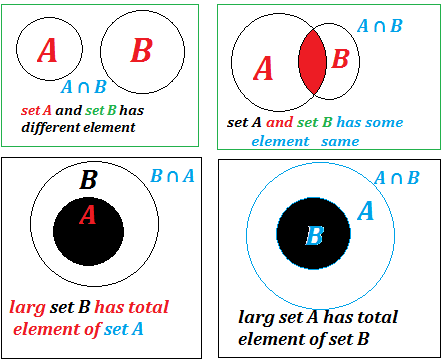
Intersection meaning in two set:
common element in the set A and B is called intersection or same element in the set A and B is called intersection, intersection in math denoted by symbol ∩
Intersection diagram in two set
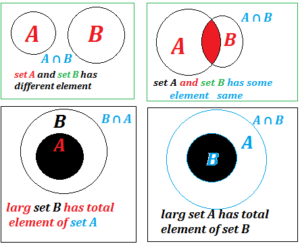
Example of intersection meaning in two set
If we have set A = {1, 3, 6, 9} and set B= {2, 3, 7, 9}
SOLUTION:
A ∩ B= {1, 3, 6, 9} ∩ {2, 3, 7, 9}
A ∩ B= {3, 9} is the intersection of set A and B.
Intersection of PHY set. φ , Or null set
Set A = {} = φ and set B = {1,6,9,10}
A ∩ B = {} ∩ {1,6,9,10}
A ∩ B = {} = φ
Intersection of same set
if we have set
A = {1,2,3,4,5,6} and set B = {1,2,3,4,5,6}
A ∩ B = {1,2,3,4,5,6} ∩ {1,2,3,4,5,6}
SO
A ∩ B = {1,2,3,4,5,6}
the result prove that when set A and Set B have number
(1) A ∩ B = A
(2) A ∩ B = B
We can write position set 1 and 2
(i) A ⊆ A ∩ B
(ii) B ⊆ A ∩ B
RELATED POST
- COMPLEX Z PLANE
- ♣
- Dimensional system
- ♠
- TYPE OF SET
- ♣
- PROPER AND IMPROPER SUBSET
- ♥
- standard equation of hyperbola math
- ⇔
- Foci of the ellipse, covert ices major and minor axis
- ⊆
- parabola 4 types concept standard form
- ⊄
- bisect the chord theorem ppt
- θ
- Algebraic function for ppt examination
- ⇐
- log rule exponential