What is quadrants Angle: When the terminal line lies on the x-axis or the y-axis, the angle theta (تھیٹا) or θ is called the quadrant angle. For example, zero degree 0 º Ninety degree 90 º two seventy degree 270 º Three sixty degree 360 º and more on is called the Example of quadrant Angle.
Quadrant Angle on Zero degree explanation:
(A) when theta = 0 º
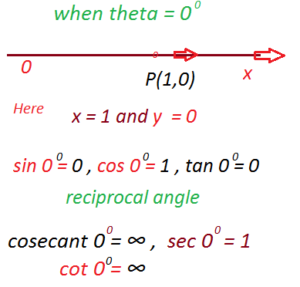
The point (1, 0) lies on the terminal side of Angle 0 º
This implies that x = 1 and y = 0
so
r = √ x² + y² =1
sin 0 º = y / r = 0 / r = 0
Reciprocal of sin 0 º
cosecant 0 º = 1 / sin 0 º = 1/ 0 = undefined
(2)
cos 0 º = x / r = 1 / 1 = 1
Reciprocal of cos 0 º
sec 0 º = 1 / cos 0 º = 1/ 1 = 1
(3)
Tan 0 º = y / x = 0 / 1 = 0
Reciprocal of tan 0 º
cot 0 º = 1 / tan 0 º = 1/ 0 = undefined
(B) when theta = 90 º
The point (0, 1) lies on the terminal side of Angle 90 º
This implies that x = 0 and y = 1
so
r = √ x² + y² =1
Trigonometric function values of 90 degree proof:
(ii) sin 90 º = y / r = 1 / 1 = 1
Reciprocal of sin 90 º
cosecant 90 º = 1 / sin 90 º = 1/ 1 = 1
(ii) cos 90 º = x / r = 1 / 0 = 0
Reciprocal of cos 90 º
sec 90 º = 1 / cos 90 º = 1/ 0 = 0
(iii)
Tan 0 º = y / x = 1 / 0 = undefined
Reciprocal of tan 0 º
cot 90º = 1 / tan 90º = 0/ 1 = 0
(C) when theta = 180 º
what is quadrants Angle values of 180 degree
The point (1, 0) lies on the terminal side of Angle 0 º
This implies that x = 1 and y = 0
so
r = √ x² + y² =1
(i)
sin 180 º = y / r = 0 / 1 = 0
Reciprocal of sin 180 º
cosecant 180 º = 1 / sin 180 º = 1/ 0 = undefined
(ii)
cos 180 º = x / r = -1 / 1 = -1
Reciprocal of cos 180 º
sec 180 º = 1 / cos 180 º = 1/ – 1 = – 1
(iii)
Tan 180 º = y / x = 0 /- 1 = 0
Reciprocal of tan 180 º
cot 180 º = 1 / tan 180 º = 1/ 0 = undefined
(D) when theta = 270 º
what is quadrants Angle values of 270 degree
The point (0, -1) lies on the terminal side of Angle 270 º
This implies that x = 0 and y = -1
so
r = √ x² + y² =1
(i)
sin 270 º = y / r = -1 / 1 = -1
Reciprocal of sin 0 º
cosecant 270 º = 1 / sin 270 º = 1/ -1 = -1
(ii)
cos 270 º = x / r = 0 / 1 = 0
Reciprocal of cos 270 º
sec 270 º = 1 / cos 270 º = 1/ 0 = Undefined
(iii)
Tan 270 º = y / x = -1 / 0 = undefined
Reciprocal of tan 270 º
cot 270 º = 1 / tan 270º = 0 /-1 = 0
RELATED POST:
Symbolic logic set theory table
Mantissa of logarithm of real number