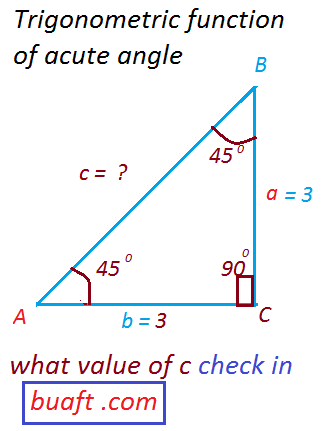
Trigonometric function of acute angle of any size:Consider a right triangle ABC with m ∠ C = 90º and sides a, b, c we write ∠ A opposite side name a and the ∠ B opposite side name b and more the ∠ C opposite side name c.
Trigonometric function of any size :
As, values of trigonometric function depend only on the angle and not on the size of the triangle. We can take any size of triangle.
When m ∠ A = 45º = π / 4 radians
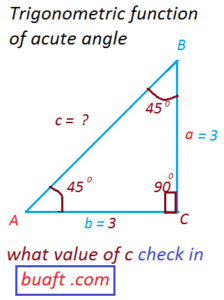
then
m ∠ B = 45º
this implies that Δ ABC is right isosceles triangle(مساوی الساقین مثلث)
Take size of triangle a = b = 3
By Pythagoras theorem:
a² + b² = c ²
putting the values
we get
(3)² + (3)² = c ²
9+ 9 = c ²
18 = c ²
Taking square root on both side
√3 ×3×2 = c ²
3 √ 2 = c ²
it is cleared the value of c
c = 3 √ 2, a = 3, b = 3
sin 45º = a / c = 3 / 3 √2
Hence
sin 45º = 1 / √2 reciprocal of sin cosecant 45º= √2
this is proved the value of the trigonometry function only depend on angle, not triangle size.
Trigonometry function of 60 degree:
when m ∠ A = 60º = π / 3 radians, then m ∠ B = 30 º
By elementary geometry, in a right triangle, the measure of the side opposite to 30 º is half (نصف)of the hypotenuse (وتر).
Let take any value c= 2 then b = 1
By Pythagoras theorem:
a² + b² = c ²
this implies that a² + (1)² = (2) ²
a² = (2) ²- (1)²
a² = 4- 1
taking square root on both side
a = √3, b = 1, c = 2
Sin, cos and tan angle on 60 degree
(1) Sin 60° = a / c = √ 3 / 2
reciprocal
cosecant 60º = 1 / Sin 60°= 2 / √3
(2) cos 60° = b / c = 1 / 2
reciprocal
sec 60º = 1 / cos 60°= 2
(3) tan 60° = a / b = √ 3
reciprocal
Tan 60º = 1 / Tan 60°= 1 / √3
Trigonometry function of 30 degree:
Trigonometric function of acute angle of any size
When m ∠ A = 30º= π / 6 radians
then
m ∠ B = 60º
By definition of elementary geometry, in a right angle triangle the measure of the side opposite (برعکس) to 30 º is a half of the hypotenuse.
Let c = 2 then a = 1
by Pythagoras theorem
a² + b² = c ²
b² = c ² – a²
= 4 – 1
= 3
b² = √ 3
now we have the value of a = 1, b = √ 3, c = 2
Sin, cos and tan angle on 30 degree:
(1) Sin 30° = a / c = 1 / 2
reciprocal Angle of sin
cosecant 30 º = 1 / Sin 30°= 2
(2) cos 30° = b / c = √ 3 / 2
reciprocal Angle cos
sec 30 º = 1 / cos 30 °= 2 / √ 3
(3) tan 30° = a / b = 1 /√ 3
reciprocal angle tan
cot 30° = 1/ tan 30 º = √ 3
RELATED POST:
Trigonometric Function of any Angle
Initial side and terminal side angle