symmetric Matrix of 3 by 3 square matrix

Symmetric Matrix of 3 by 3 square matrix: A square matrix 2×2 or 3×3 ……………..n×n is a symmetric matrix. If the transpose of this matrix is equal to the original matrix. Example transpose of B = B

KEEP IN MIND:

1. In addition and subtraction of two symmetric matrixes, the result is always a symmetric matrix.
2. Always two symmetric matrixes verify the commutative property that is AB =BA 
3. Always B is a symmetric matrix has inverse B¯ ¹ also symmetric

Transpose matrix mean:

Change the number of rows in the column or number of column into rows is called transpose matrix

Square matrix mean:

If a matrix has the number of rows and number of column are equal, is called square matrix.

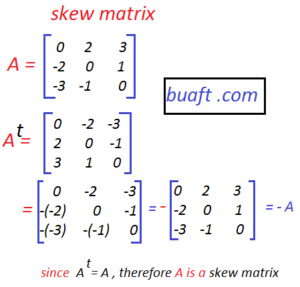
Skew symmetric matrix.

A square matrix B is said to be a skew – symmetric.

If B transpose = – B

KEEP IN MIND:

1. Scalar multiplication of a Skew matrix is also a Skew matrix.
2. Addition of Skew matrix and identity matrix is also a skew matrix.
3. Skew symmetric matrix determinant is always non-negative.
4. Diagonal entries in Skew symmetric matrix has consisted of zero element.

Negative of a matrix:

A matrix multiplied by negative all entries then matrix is called negative matrix.