In everyday use relations concept means an abstract type of connection between two person or objects, for stance (teacher, poor), (mother, son), (husband, wife), (brother, sister), (friend, friend), (house, owner) in mathematics also some operations determine relationship between two numbers for example.Relations concept example in math example.
(1) Greater than : (5,4) or greater than sign mean > in math
(2) square: (25,5)
(3) square root: (2,4)
(4) equal : (2×2,4)
A relation is a set of ordered pair whose element are ordered a pair of relation number of objects. The relationship between the component of an ordered pair may or may not be mentioned.
RELATIONS CONCEPT POINT
(a) BINARY RELATION:
Let any set A and B be two non-empty, then any set of the Cartesian products A×B is called a binary relation or simply a relation from A to B.
(b) DOMAIN:
The set of the 1st element of the ordered pair forming a relation is called its domain.
(c) RANGE:
The set of 2nd elements of the ordered pairs formed a relation is called its range.
(d) RELATION ON A
If A is a non-empty set, any subset of A×A is called a relation in A OR on A
EXAMPLE
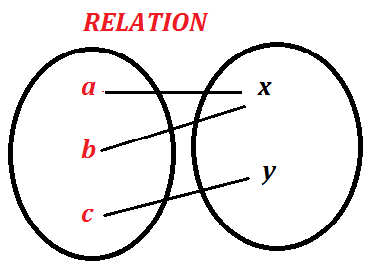
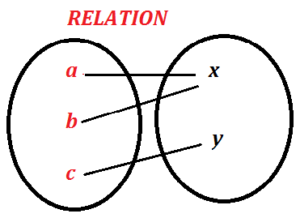
Let a, b, c be three children and x, y be two men such that father of two children a, b is x and father of c is y.
Defined relation between.
SOLUTION:
C= set of children = {a, b, c} and F= set of fathers= {x, y}
C×F = {(.a, x), (.a, y), (b, x), (b, y), (c, x), (c, y)}
r = set of ordered pairs (children, father)
= C×F = {(.a, x), (b, x), (c, y)}
DOM r = {a, b, c}, Ran r = {x, y}
EXAMPLE: 2
Let A = {1,2,3} Determine the relation r such that x relation y,
Iff x< y
SOLUTION:↔
A×A={(1,1), (1,2), (1,3), (2,1), (2,2), (2,3), (3,1), (3,2), (3,3)}
clearly required relation is such that
r= {(1,2), (1,3), (2,3)}, Domain. r.={1,2} Ran r= (2,3)
RELATED POST: