power set of empty set,, power set of empty set is a singleton set. Let B = { } OR B = φ , then B has only one possible subset that is
P(B) = { φ }
power set of a set collection of all possible subset of any set A is called power set of A denoted by P(A). For example ,A = {3,4} then all possible subset of A are : A= { } {3 } , {4 }, { 3 , 4}.
Remember that:
Let n (a) =m (number of elements in A is m). then number of power set n p (A )= 2 power m ( n umber of element of P(A)
(1) A = { } because number of element in A = 0 mathematically denoted by n (A) = 0 And number of power set is denoted by mathematically n P(A)= 2⁰ =1
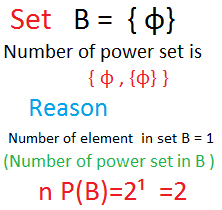
(2) B= {0,1} because number of element in B = 0 mathematically denoted by n (B) = 2 And number of power set is denoted by mathematically n P(2)= 2² =4
(3) C= {1,2,3,4,5,6,7} because number of element in C = 7 mathematically denoted by n (C) = 7 And number of power set is denoted by mathematically n P(7)= 2⁷ =128
(4) D= {0,1,2,3,4,5,6,7} because number of element in D = 8 mathematically denoted by n (D) = 8 And number of power set is denoted by mathematically n P(8)= 2⁸ =256
(5) E= { a,{b,c} } because number of element in D = 2 mathematically denoted by n (E) = 2 And number of power set is denoted by mathematically n P(2)= 2² =4
(6) F= {{a,b},{b,c},{d,e} } because number of element in F = 3 mathematically denoted by n (F) = 3 And number of power set is denoted by mathematically n P(3)= 2³ =8
Write down the power set of each set
Q : 1
A = { 9, 11}
Number of power set is
{ φ , {9},{11},{9,11} }
Reason
Number of element in set A = 2
(Number of power set in A) n P(A)= 2² =4
Q : 2
B = { φ}
Number of power set is
{ φ , {φ} }
Reason
Number of element in set B = 1
(Number of power set in B ) n P(B)=2¹ =2
Q : 3
C = { a,{b,c}}
Number of power set is
{ φ , {a},{b,c},{a,{b,c} }
Reason
Number of element in set C = 2
(Number of power set in C) n P(C)=2² =4
RELATED POST
complement of a set symbol
proper and improper subset example