Linear inequalities in ordered pair(1)The set of ordered pair (x, y) such that ax+by < c (2) And the set of ordered pair (x, y) such that ax+by > c the region one and two are called half plane and the line ax+by=c is called the boundary of each half plane.
Vertical line in Linear inequalities ;
a vertical line divides the plane into left and right half plane.
NON-Vertical line in Linear inequalities ;
non-vertical line divides the plane into upper and lower half planes.
A solution of linear inequalities in x and y ordered pair of number, which satisfies the inequalities.
Linear inequalities in ordered pair:
EXAMPLE:
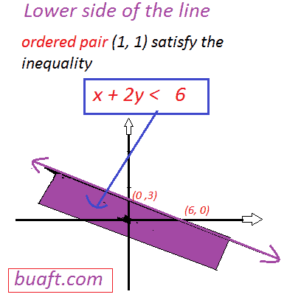
The ordered pair (1, 1) is a solution of the inequality x + 2y < 6 because 1+ 2(1)=3 < 6 which is true.
There are inequalities many ordered pairs that satisfy the inequality x + 2y < 6, so its graph will be half plane.
Corresponding Equation in inequalities:
Linear inequalities ax +by =c is called associated Or corresponding equation of each of the above-mentioned inequalities.
EXAMPLE:
Graph of inequality x + 2y < 6
SOLUTION:
The associated equation of inequality.
(i) x +2y < 6
is
x + 2y = 6
the line (ii) intersect the x-axis and y-axis at (6, 0) and (o, 3) respectively. As no point of the line (ii) is a solution of the inequality (i) , so the graph of the line (ii) is shown by using dashes. We take o(0, 0) is a test point because it is not on the line (ii)
substituting x =0, y = 0 in the expression x = 2y gives 0 – 2(0) =0<6 so the point (0,0) satisfies the equation (i)