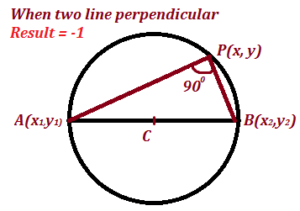
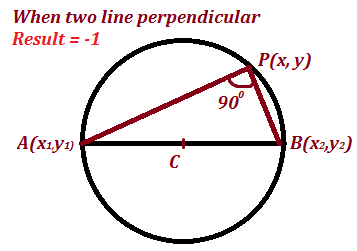A circle passing through two point and having its center on the line. An equation of circle having the join of A(x₁, y₁) and B(x₂, y₂) as a diameter
Since line AB is a diameter of the circle. Its midpoint is the center of the circle. The radius of the circle is known, as the standard form of an equation of the circle may be easily written. However, a more elegant procedure is to make use of the plane geometry. If P(x, y) is any point on the circle,
then
m ∠ APB=90
Thus, the line AP and BP are perpendicular to each other.
and
When line are perpendicular to each other, the resulting value is negative
After simplification, we can be written as
This is the equation of a circle passing through two point, having its center on the line.
Example:
A circle passing through two point and having tangent at one of these points is known.
For example, equation of the circle passing through the point (-2, -5) and touching the line 3x+4y-24=0
at the point (4, 3)
Solution:
We know that the equation of circle
…………………a
The points (-2, -5) and (4, 3) lie on it. Therefore
-4g-10f+c+29=0……………………………………….b
8g+6f+c+25=0……………………………………..c
the line
3x+4y-24=0……………………………..d
touch the circle at (4,3)
A line through (4, 3) perpendicular to (d)
4x-3y+7=0
This line being a normal through (4,3) passes through the center
(-g, -f) of the circle (a)
-4g+3f-7=0…………………. e
From (b)- (c), we get
-12g-16f +4=0
or
3g+4f-1=0……………………f
By solving equation (e) and (f) we get
g=-1, f=1
putting the value of g and f into equation (c)
the resulting value of c= -23
thus the equation of circle is
RELATED POST:
%0