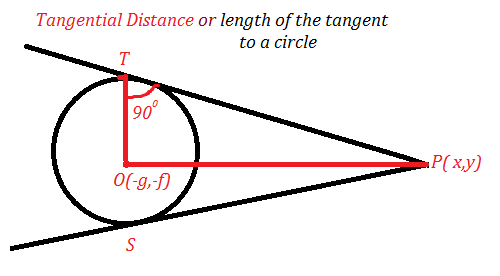
The point of contact of tangent with the circle at point S and T. then each of the length PS and PT is called tangential distance from P to the circle. More explanation,
Suppose that we have any point outside the circle p(x₁, y₁). Then equation of form is
x²+y²+2gx+2fy+c =0…………………….. A
we know that two real and distinct distance can be drawn to the circle from an external point. If the point of contact of these tangent with the circle are S and T. then the length PS and PT is called the length of the tangent or tangential distance from P to the circle A.
The center of the circle has coordinated (-g, -f) joint PO and OT. From right triangle OTP
Tangential distance =
=
We can also find the tangential distance PS from this formula.
Tangential distance example:
EXAMPLE :1
Fined the length of the tangential distance from the point P(-5, 10) to the circle
5x²+5y²+14x+12y-10=0
solution:
Equation of the given circle in standard form is
dividing both side of equation by 5
x²+y²+14/5 x+12/5y-2=0……………(A)
Square the length of the tangent from point P (-5, 10) to the circle. A is obtained by substituting
X = -5
y= 10
we get length of the tangential distance
tangential distance =
CORD OF CONTACT:
Example:
Tangent are drawn from (-3. 4) to the circle x² + y² = 21. We fined an equation of the line
joining the point of contact. This line is called the chord of contact.
Solution:
let the point of contact of two tangent be P(x1, y1) and Q (x2, y2)
An equation of tangent at point P is
XX1+yy1= 21………………….a
An equation of tangent at point Q is
XX2+yy2 = 21 ……………………b
since (1) and (2) pass through (-3,4), so
3×1+4y1=21………………. c
and
-3×2+4y2=21………………’d
(c) and (d) show that the both point
P(x1, y1), Q(x2, y2) lies on -3x+4y=21
and so it is the required equation of chord of contact.
RELATED POST: