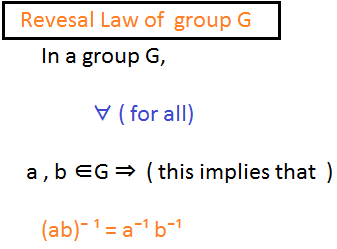Reversal law of inverse

Reversal law of inverse statement: In a group G, ∀ ( for all) a , b ∈ G ⇒ ( this implies that  )

(ab)⁻ ¹ = a⁻¹ b⁻¹

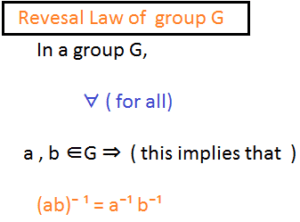
Proof:

Since   ab(ab)⁻ ¹ = e ( means identity)

multiplying both sides a⁻¹

a⁻¹ab(ab)⁻ ¹ =a⁻¹ e

 because a⁻¹a  = e

e b (ab)⁻ ¹   =  a⁻¹ e

 b (ab)⁻ ¹   =  a⁻¹

Again multiplying both sides b⁻¹

b⁻¹ b (ab)⁻ ¹   =  b⁻¹a⁻¹

 because b⁻¹b  = e

e (ab)⁻ ¹   =  b⁻¹a⁻¹

 (ab)⁻ ¹   =  b⁻¹a⁻¹

∵ e is identity element

Reversal law of inverse  complete the proof

Related post:

power set of empty set

difference of two set

singleton set has proper subset