Ellipse in standard form concept
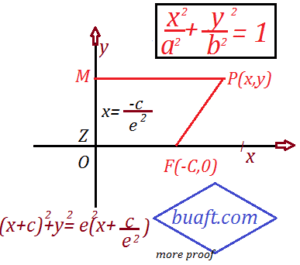
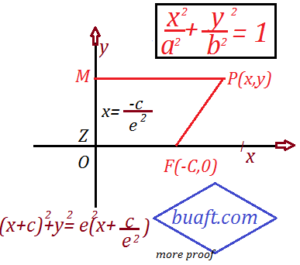
Let F(-c, 0) be the focus and the line x = -c / e ² be the directrix of an ellipse with the eccentricity e that is (0, e < 1). Let p(x, y) be any point on the ellipse and suppose that |PM| is the perpendicular distance of P from the directrix then.
|PM| = x + c / e ²
The condition |PF| = e |PM|
Analytic form:
(x+c)² +y² = e² (x + c / e ²)²
x²+2.c.x+c² + y²= e²x²+2 c.x + c ² / e²
x ² (1 – e ²) + y² = c² / e ²(1 – e²)
x ²(1 – e²) + y ² = a ² (1 – e ²)
where c / e = a
x ² / a ²+ y² / a² (1 – e²) = 1………………… A
if we write
b² = a ² (1 – e²)
then equation A become
………………… B
Which is an equation of standard form.
Eccentricity of the ellipse is e = c / a
We have
b² = a ² (1 – e²)
= a ² – a ² e²
= a ² – c ²
Eccentricity when b < a, of ellipse:
(i) from, the relation b² = a ² (1 – e²) we note that b < a
(ii) since we have c / e = a , the focus F has coordinated (- a.e, 0) and the equation
of the DirectX is x = – a / e
Foci of an ellipse:
(iii) If we take the point (a.e, 0) as focus and the line x = a / e as DirectX, it can be seen easily
that, we again obtained equation A. thus the standard form of ellipse has two Foci (- a.e, 0) and (a.e, 0)
and two directrix X = ± a / e
Parametric form of an ellipse from equation B:
ellipse in standard form more concept:
The point (a cos θ, b sin θ) lies on equation A for all real θ
Where
X = a cos θ
Y = b sin θ
If we put b = a, in equation B then it becomes
x² + y² = a ²
Which is a circle. In this case, b² = a ² (1 – e²) = a ² and e = 0.
Thus, a circle is a special case of an ellipse with eccentricity 0 and Foci tending to the circle