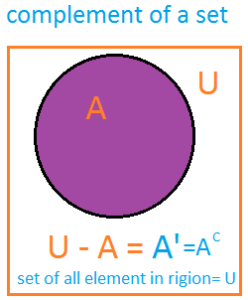
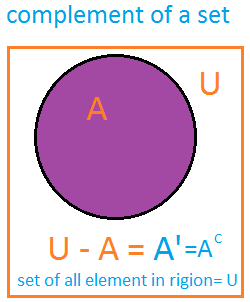compliment of a set A , denoted by A’ . or A compliment relative to the universal set U is the set of all element U , which do not belong to A.complement of a set symbol : A’ = { x | x ∈ U ∧ x ∉ A }
Explanation A compliment equal to: x :such that: x is a member of U and x is not a member of A.
complement of a set symbol
For Example:
If Set U = N ( is the set of natural number)
E ‘ = O ( even number compliment = odd number)
O ‘ = E ( odd number compliment = even number)
Example: If U = { 1, 2,3,4,5,6,7,8,9 }
E’ = U – E = O
E’ = { 1, 2,3,4,5,6,7,8,9 } – { 2, 4,6,8 } = { 1, 3, 5 ,7,9} = ODD number
For Example:
If Set U = N ( is the set of natural number)
E ‘ = O ( even number compliment = odd number)
O ‘ = E ( odd number compliment = even number)
Example: If U = { 1, 2,3,4,5,6,7,8,9 }
O’ = U – O = E ( even number)
O’ = { 1, 2,3,4,5,6,7,8,9 } – { 1,3,5,7,9 } = { 2,4,6,8} = Even number.
Overlapping Sets:
If the intersection of two sets is non empty ( have number) but neither is a subset of the other, The set is called overlapping sets, Example on;
L = { 2,3,4,5,6} and M = { 5,6,7,8,9,10} then L and M are two overlapping set;