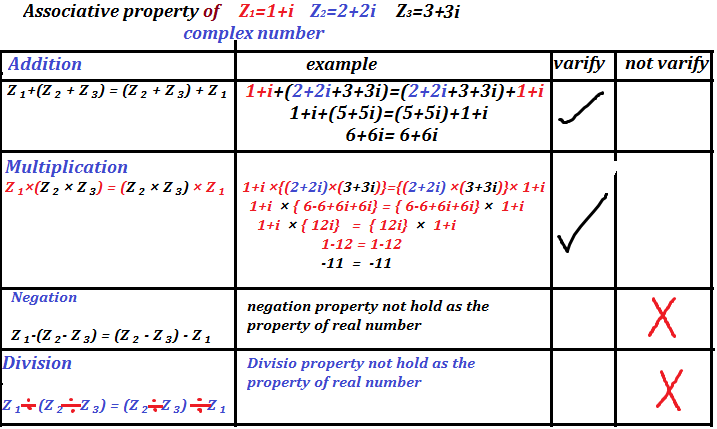
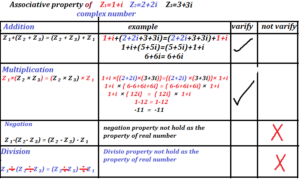
Associative property of complex number addition, multiplication, negation, division verify or not verify on addition, multiplication, negation, and division. If we have three complex numbers z ₁ = a+ι b, z ₂=c + ι d, and z ₃=e+ι f then the association of these three complex number hold or not hold we separately check one by one
Association of complex number Addition:
Z ₁+(Z ₂ + Z ₃) = (Z ₂ + Z ₃) + Z ₁……………………… A
putting the value of
z ₁ = a+ι b,
z ₂=c + ι d,
and
z ₃=e+ι f
In Equation A
a+ι b +(c + ι d + e+ι f) = (a+ι b +c + ι d) + e+ι f
a+ι b +c + ι d + e+ι f = a+ι b +c + ι d + e+ι f
Association of complex number Addition example
For example: if we take three numeric complex
z ₁ = 6+7ι
z ₂= 4+9Ι
and
z ₃= 1+8Ι
Putting these complex number values in A
6+7ι +(4+9Ι + 1+8Ι) = (6+7ι +4+9Ι)+ 1+8Ι
6+7ι +(5+17Ι) = (10 +16Ι) + 1+8Ι
11 +24ι = 11+ 24 Ι
This is clearly showing that association of three complex number addition hold.
Association of complex number multiplication:
Z ₁×(Z ₂ × Z ₃) = (Z ₂ × Z ₃) × Z ₁……………………… B
z ₁ = a+ι b,
z ₂=c + ι d,
and
z ₃=e+ι f
In Equation B
a+ι b ×{(c + ι d) ×(e+ι f)} ={(a+ι b) × (c + ι d)} ×(e+ι f)
We know that direct multiplication rule of complex number
a+ι b ×(c e – d f+ ι c f+ι d e) =( a c -b d +ι ad + ι b c) × (e+ι f)
Again, multiplication of complex number in two sides
a c e -a d f +ι a c f + ι a d e + ι b c e – ι b d f – b c f – b d e = a c e – b d e + ι a d e +ι b c e + ι a c f – ι b d f – a d f – b c f
a c e -a d f – b c f – b d e +ι a c f + ι a d e + ι b c e – ι b d f = a c e – a d f – b c f- b d e+ ι a d e +ι b c e + ι a c f – ι b d f
Hence, two sides are equal association of multiplication hold
RELATED POST